NOTE: This preliminary draft has been revised and expanded. The finished article can be seen here.
The preceding post, Part 7, introduced some concepts applicable to complex system analysis. These included representations of reality and a property called ergodicity. This article delves more deeply into the challenges that arise from these sources in modeling complex systems.
Introduction
This section discusses how the description of the process and results of repeatedly flipping a coin three times is much more complex than might be assumed. The process involves complicated combinatorial calculations. This makes it problematic to define ergodicity in a meaningful way. Examining alternative definitions of ergodicity proves helpful. Then, we look at some problems that arise in the analysis of other complex systems.
Complexity in the process of flipping three coins
The process of flipping a coin three times has eight possible sequences. From Part 7, we have a probability array for the eight sequences.
This array of the eight possible sequences does not represent what someone expects when exercising eight successive three-flip sequences. The reason is obvious. All eight possible outcomes are equally likely every time there are three coin flips. That makes the process the same as picking one of eight objects out of a bag eight times, with replacement after each pick.
Part 4 shows that there are 6,435 possible outcomes for making three coin flips eight times. The probability array is one of those outcomes. Part 5 shows how the eight sequence outcomes are distributed among 22 types that are differentiated by how individual sequences are distributed among various repetition patterns that can occur. Part 6 shows that the probability of the probability array as an outcome for producing eight sequences is 0.24%. Thus, the probability of obtaining some other outcome is 99.76%.
This complexity makes clear that using the probability array as the basis for modeling processes involving three coin flip sequences is ill-advised. The probability array is a basis for predicting the outcome of a large number of sequences. This is shown to be of the order of a few hundred to 1,000 sequences for an approximate prediction and as many as 10,000 sequences or more for an accurate prediction. However, modeling using probability will be unsuccessful in following a pathway from a few flipping sequences out to several hundred and beyond, as experimental results differ widely from the probability average.
More on Ergodicity
Ergodicity is defined in a number of different ways. Part 7 reviewed ergodicity based on the definition that ergodic systems have the spatial average of a property at any given time being the same as the average of that property over time. Two examples were the behavior of electrons in atoms and molecules and pressure in a closed gas container (constant volume) held at constant temperature.
How the usefulness of ergodicity is compromised in the coin-flipping process
We previously stated that the current system of three coin flips repeated many times involves an ergodic process. The long-time average of thousands of three-flip sequences and the spatial average represented by the probability array are the same.* However, the averages over intermediate times can vary widely from the spatial average. This may reflect that the coin-flipping process here corresponds to von Neuman’s mean ergodic theorem rather than Birkhoff’s pointwise ergodic theorem. This question goes beyond the scope of the analysis attempted here. We only need to recognize that the possible pathways from a few sequences to hundreds and thousands of sequences are not ergodic: Many different pathways are possible. While the average of all the possible pathways may be ergodic (not proven in this study), our concern is what happens to a person conducting multiple coin flips – not the average of all people flipping coins.
*To be rigorously correct, the long-time and spatial averages are nearly the same. The long-time average approaches the spatial average with large numbers of sequences over time. However, it appears that the two averages will never be identical no matter how large the number of sequences becomes.
Problematic situations with assumed ergodicity
We see above the problems that arise with non-ergodic behavior with shorter-term accumulations of coin-flipping sequences by an individual coin flipper. How does this relate to other analysis situations?
Modern Portfolio Theory
Modern Portfolio Theory proposes that an investor can construct a portfolio of multiple assets that will result in greater returns without a higher level of risk. The investor portfolio is constructed based on market data for some selected period of past performance. The father of the theory is Harry Markowitz, who first published on MPT in 1952 and was awarded the Nobel Prize in 1990. The theory’s essence is that a portfolio’s expected return is a weighted sum of the past returns of the individual assets. The risk in the portfolio is the variance of past returns.
The implicit assumption is that both risk and return on investment assets are ergodic: The average of past risks and returns (spatial averages) will be the same as future returns. This assumes ergodicity. There is little more to say about this than to quote the legal disclaimer required by the US Securities and Exchange Commission (SEC): SEC Rule 156 requires mutual funds to tell investors not to base their expectations of future results on past performance before they invest.
MPT and individual investors
There is another aspect of problems with MPT as it pertains to individual investors. Even if the prediction of expected returns and risks for the market were reliable, they would not apply to individual investors. All investors comprise the market. The data for the market is effectively that of the average investor. An individual investor can fall anywhere on the distribution curve of results for all investors. MPT appropriately provided justification for the development of market index funds. These funds provide an investor with the expectation of receiving a market return.
The often-quoted comment that MPT proves that no one can “beat the market” over time is simply false. Warren Buffet and Peter Lynch are two very public examples of that. The correct statement is that the average investor cannot beat the market over time: The average of all investors defines the market.
Going broke on a sure thing
Ole Peters is a physicist and the program lead for ergodicity economics at the London Mathematical Laboratory. He is also an external professor at the Santa Fe Institute. In 2014, he published a paper with Nobel Prize-winning physicist Murray Gell-Man, Evaluating Gambles Using Dynamics. The journal Chaos published the paper in February 2016. It was the most-read paper of 2016 in that journal. The further work discussed here follows from that paper.
Consider the process of a series of single coin flips such that a head increases one’s wealth by 50% and a tail decreases it by 40%. This sounds like a sure winner. How can you lose?
Ergodicity (or lack thereof) rears its ugly head here. The graph below shows the blue line if one runs a simulation using an infinite ensemble (all possible outcomes). This is a spatial array of all possibilities. However, when one runs simulations of individuals following the same series of coin flips, the usual outcome shows trajectories that all lose money.
Randomly generated trajectories of the repeated example gamble.
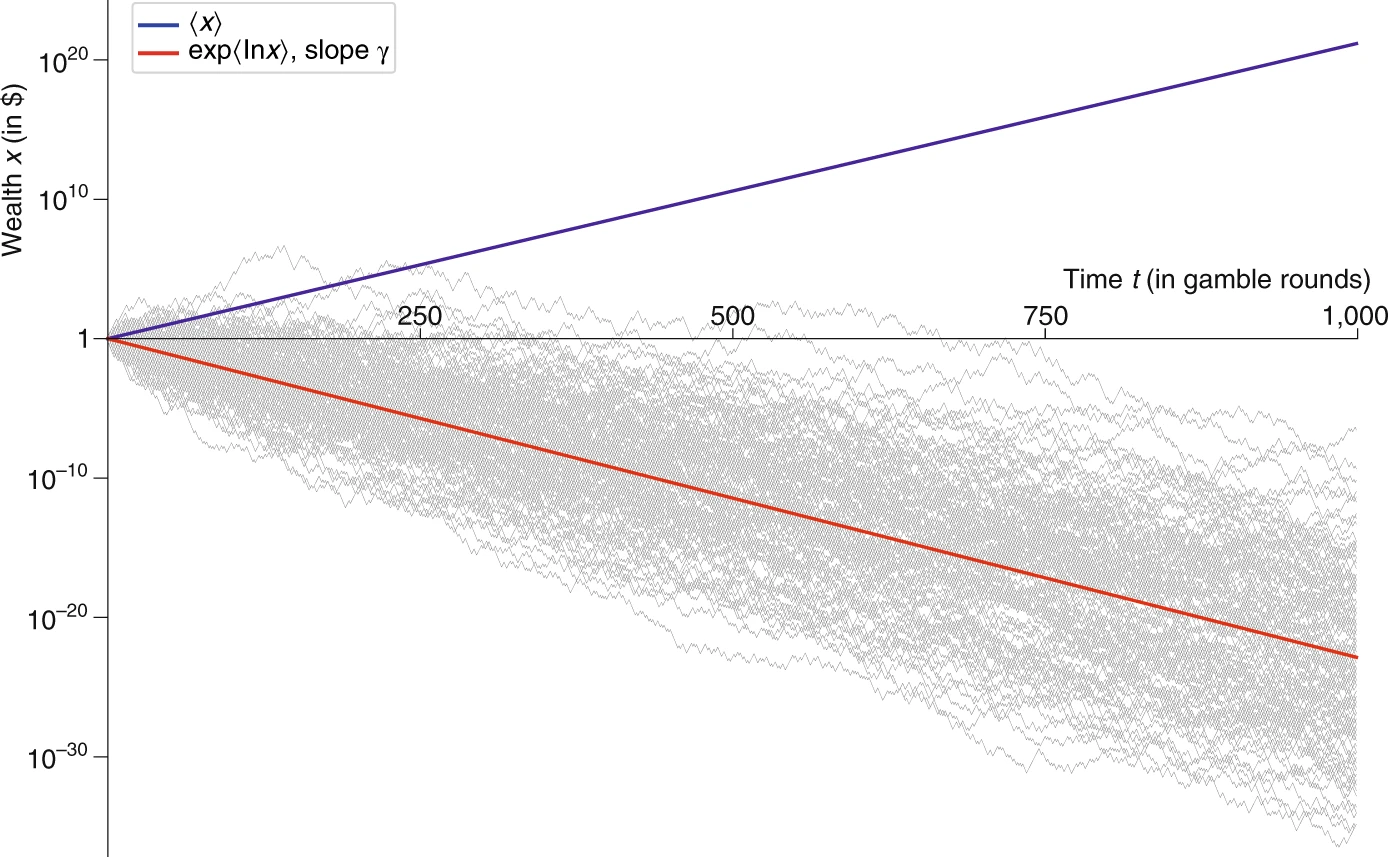The example gamble is given in equation (2). The expectation value, 〈x〉, (blue line) is
the average over an infinite ensemble, but it doesn’t reflect what happens over time.
The ergodic growth rate for the process (slope of the red line) tells us what happens to
a typical individual trajectory. 150 trajectories are shown, 1,000 repetitions each.
The infinite ensemble
Peters explains the rising wealth of the infinite ensemble:
Let’s start with averaging wealth, over an ensemble of many different systems. In our case, this corresponds to N different players, each starting with $100, say, and each tossing a coin independently. After the coins have been tossed, about half of the people will have thrown heads and the other half tails. As the number of players goes to infinity, the proportions of heads and tails will approach 1/2 exactly, and half the players will have $150, the other half $60. In this limit, we know what the ensemble average will be, namely 1/2($150+$60)=$105. For historical reasons, this average is also called the expected value, and for the Peters coin toss, it grows by 5% in every round of the gamble so that $100×1.05.
The individual experience over time
But for the individual coin tossers:
Here, as T grows, again the proportions of heads and tails converge to 1/2. But, crucially, a head and a tail experienced sequentially is different from two different agents experiencing them. Starting at $100, heads takes us to $150, and following this sequentially with tails, a 40% loss, takes us down to $90 — we have lost 10% over two rounds, or approximately 5% per round. Since we lose 5% per round, averaged over time, individual wealth is guaranteed to approach zero (or negative infinity on logarithmic scales) in the long-time limit .
This breakdown of ergodicity differs from our exercise of flipping a coin three times because, in our scenario, the probability array defines a finite spatial array. In our situation, individual coin flippers’ deviations deviate from the long-term time average. However, Fix‘s simulations show that at sufficiently long times, the time average of results converges back to the spatial average. So, our coin-flipping process is ergodic with intermediate time frame exceptions.
Can a process with an infinite ensemble ever be ergodic?
I have seen a paper that I believe gives such an example. With the caveat that this is from memory, the example was similar to the Peters example above. The difference was that there was a 50% probability of a 60% gain and a 50% probability of a 40% loss. My recollection is that this formulation produced a 20% probability of individuals going broke. Search as I might, that reference is still missing. Thus, the answer to the question has to be maybe for now.
A Random Walk Down Wall Street and Skin in the Game
Part of the title of this section is the same as a book by Burton G. Malkiel. In the book, Malkiel explains why a well-diversified portfolio is likely to exceed the performance of portfolios carefully picked by professionals. The second part of the title is the same as a book by Nassim Nicholas Taleb. Taleb gives insight into the reasons why Malkeil’s observations are related to ergodicity.
Taleb points out that investing success requires survival, i.e., not losing all your money. When the stock market goes up, that does not mean that all investors are successful unless they invest in the market index. If risk is greater than the market risk, volatility will create a series of gains and losses. Only those lucky enough to get the providence of favorable ordering of gains and losses will be successful. See this excerpt from Skin in the Game in Medium for a good insight into Taleb’s arguments. Taleb specifically discusses the paper by Peters and Gell-Mann, cited in the preceding section.
Modeling the effects of climate change
Discussion to be added.
Complex Systems and Rational Expectations
The coin three coin flipping analysis is an example of a complex system. It is simpler than many complex systems because we know the probability of elemental steps, process sequences, and large sample results. Such probabilities are unknown in many other complex systems, and we must estimate or assume them. The limited applicability of ergodicity discussed above sets the table for discussion of other complex systems.
Are statistical models reflecting rational expectations?
This discussion to be added.
How does the DSGE** modeling process relate to reality?
This discussion to be added.
Can the observations of a microsystem establish a reliable basis for modeling a macro system?
This discussion to be added.
Concluding Thoughts
Conclusions will be added in the next (hopefully final) pass next week.
**DSGE: Dynamic Stochastic General Equilibrium
Caption photo by Pixabay.
Previous Articles in the Series
Part 1: The Gamblers’ Paradox.
… Lounsbury, John, “Adventures With 3 Coin Flips. Part 1: The Gamblers’ Paradox,” EconCurrents, May 21, 2023, https://econcurrents.com/2023/05/21/adventures-with-3-coin-flips-part-1-the-gamblers-paradox/
Part 2: Connecting the Micro to the Macro.
… Lounsbury, John, “Adventures With 3 Coin Flips. Part 2: Connecting the Micro to the Macro,” EconCurrents, May 28, 2023, https://econcurrents.com/2023/05/28/adventures-with-3-coin-flips-part-2-connecting-the-micro-to-the-macro/
Part 3: Possibilities vs. Realities.
… Lounsbury, John, “Adventures With 3 Coin Flips. Part 3: Possibilities vs. Realities,” EconCurrents, November 19, 2023, https://econcurrents.com/2023/11/19/adventures-with-3-coin-flips-part-3-possibilities-vs-realities/
Part 4: Learning to Count at an Advanced Age.
… Lounsbury, John, “Adventures With 3 Coin Flips. Part 4: Learning to Count at an Advanced Age,” EconCurrents, November 26, 2023, https://econcurrents.com/2023/11/26/adventures-with-3-coin-flips-part-4-learning-to-count-at-an-advanced-age/.
Part 5: Identifying and Counting Outcomes.
… Lounsbury, John, “Adventures with 3 Coin Flips. Part 5: Identifying and Counting Outcomes,” EconCurrents, December 3, 2023, https://econcurrents.com/2023/12/03/adventures-with-3-coin-flips-part-5-identifying-and-counting-outcomes/.
Part 6: Probabilities.
… Lounsbury, John, “Adventures With 3 Coin Flips. Part 6: Probabilities,” EconCurrents, December 17, 2023, https://econcurrents.com/2023/12/17/adventures-with-3-coin-flips-part-6-probabilities/.
Part 7: Reality and Ergodicity.
… Lounsbury, John, “Adventures With 3 Coin Flips. Part 7: Reality and Ergodicity,” December 31, 2023, https://econcurrents.com/2023/12/31/adventures-with-3-coin-flips-part-7-reality-and-ergodicity/.
