The complexity of analyzing a process as simple as flipping a coin three times raises concerns about how to describe reality in modeling. In dealing with coin flips, we have a known probability for the result of each flip. Also, many modeling scenarios may have more than three elementary steps. Additionally, the probabilities associated with elementary steps may not be known. How does this complicate the modeling process? This review will address that question with specific emphasis on social science models, especially economics.

Introduction
Australian economist Jason Collins has considered a coin-flipping problem involving three flips per sequence. He presented a puzzling problem: Why does it appear that the probability of a head being followed by another head is 0nly 42% in the case of a three-flip sequence? After all, the probability of any coin flip is divided 50/50 between heads and tails. Economist Blair Fix considered the inverse relationship compared to Collins. He set the problem up to consider the probability that tails would follow heads. The result is 58%, complementary to Collins’ 42% for heads following heads.
The work of Collins and Fix intrigued me, and I contacted Fix with questions. As a result of our conversations about my questions, Fix suggested I try to learn more about what important lessons might be learned from a deeper dive. This work has been presented in the six previous sections of this series (list at the end of this article). This final part of the series discusses what was learned in the effort and what inferences might be made to modeling problems in social science, especially economics.
Sample Selection
The example studied in his series involved a sample consisting of three coin flips. There are eight sequences possible for the three flips. An analysis was made of the probability of a tail following a head for each of the possible sequences. The result was a 58% probability that a tail would follow a head. This disagrees with the known probability that every coin flip is 50/50.
This dichotomy is the result of sample selection. This is best understood by looking at two diagrams from Part 2:
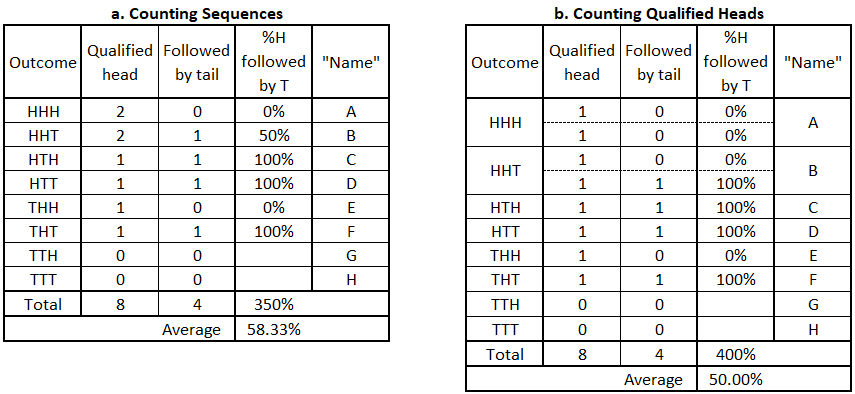
In Table a, six sequences are counted, yielding 350%/6 = 58.33…%. But in Table b, eight qualified heads are counted, yielding 400%/8 = 50%.
If one wants to characterize coin flip sequences, Table a makes sense. But if one wants to characterize individual coin flips, Table b is appropriate. How samples are selected and treated must relate appropriately to the objective of the experiment.
What is Reality?
There are eight possible sequences for three coin flips. Each has a probability of 1/8 (12.5%). The following table is a probability array showing these relationships.
How does reality relate to probability?
The probability array does more than describe the probability of obtaining each sequence when conducting three coin flips. The array also defines reality in processes consisting of three coin flips. (For the rest of this discussion, we use the term sequence to mean the sequence of flipping a coin three times.)
If one flips to create eight sequences, the eight sequences can be any combination selected from the set {A,B,C,D,E,F,G,H}. Because we must allow for all of the eight sequences, the eight-box array is the correct unit to define outcomes in scenarios involving many flips. Thus, the size of the probability array defines the dimension of the outcome unit for large systems. This completes the definitions needed for analysis of what happens (reality) in large systems of coin flips counted as three-flip sequences:
- Element: One coin flip.
- Sequence: Three coin flips.
- Outcomes: Twenty-four coin flips (3 x 8)
The relationship between probability and reality in this coin-flipping exercise will be discussed further next week.
Models that reflect reality
One can model a system to define a final state. If the probability array is defined as it is in the coin-flipping scenario, the final state after a sufficiently large number of sequences must comply with the initial array. This is hardly a very productive process except for very limited results. For example, Fix‘s model used random number generation to select successive sequences up to a large number. This process provided only one result: an approximate number of sequences necessary to approach the elemental probability in his array. (See Table a. counting sequences, above.) Little was learned about the process along the way, except for showing one particular pathway to get to the stable large sequence result.
A meaningful process model could have been developed if there were a criterion to define success or failure along the path before reaching the stable large sequence result. Then, multiple random number-generated paths could have been created. A large enough number of such paths would have provided a basis for estimating the probability of achieving successful paths. Rather than create a hypothetical situation for coin flipping, a discussion of the pathway analysis problem is better left to an analysis of investment portfolios, which will come later.
Ergodicity
Introduction of the term
From Stephen Ashley:
Ergodicity was first introduced by the Austrian physicist Ludwig Boltzmann in the 1870s, following on the originator of statistical mechanics, physicist James Clark Maxwell. Boltzmann coined the word ergodic—combining two Greek words: ἔργον (ergon: “work”) and ὁδός (odos: “path” or “way”)—to describe his hypothesis.
Etymology of ergodic
The prefix er- is used in several languages. Let’s first consider German, the language of Ludwig Boltzmann. The meaning most applicable in this case is a verbal prefix signifying a notion of getting something by some means, usually through conscious effort. This has a clear relationship to “work” in the sense of Boltzmann. But Boltzmann’s construction used er- as a prefix for a noun (“path” or “way”), so the etymology is confused. Boltzmann’s construction can be shown as ergon+odos, so he clearly was not directly considering the prefix er-. The combination of the Greek words is “ergonodos”, which simplifies to “ergodos” or “ergodic.”
The word base “godic” does not appear to have an etymological presence. It is tempting to make a connection to “godly” and “godicity” to “godliness.” However, no reference found by this author makes those connections.
Definition of ergodicity
As mentioned above, Ludwig Boltzmann introduced the term “ergodicity” about 150, years ago. His attempts to define what the word meant in relating physical, mathematical, and statistical processes met with problematic results. It was more than half a century later, in the early 1930s, that a clearer definition emerged:
The path toward greater theoretical rigor, explains University of Warwick mathematics professor Tom Ward, reached a key milestone in the early 1930s when American mathematician George D. Birkhoff and Austrian-Hungarian (and later, American) mathematician and physicist John von Neumann separately reconsidered and reformulated Boltzmann’s ergodic hypothesis, leading to the pointwise and mean ergodic theories, respectively.
— From Stephen Ashley
Birkhoff and von Neumann
The work of Birkhoff and von Neumann has been reviewed by Calvin C. Moore:
… these two papers provided a key insight into a 60-y-old fundamental problem of statistical mechanics, namely the rationale for the hypothesis that time averages can be set equal to phase averages, but also initiated a new field of mathematical research called ergodic theory, which has thrived for more than 80 years. Subsequent research in ergodic theory since 1932 has further expanded the connection between the ergodic theorem and this core hypothesis of statistical mechanics.
Birkhoff and von Neumann succeeded in describing the conditions for spatial representations of a system at any given time to be equivalent to the progression of the system through time.
Hence, the ergodic theorem transforms the question of equality of time and phase averages into the question of whether the one-parameter group representing the time evolution of the system is metrically transitive.
Ergodicity, in simple terms
A system is ergodic if the average of all the states of the system at a given time is the same as the average of one state over a long period of time. By this definition, our coin-flipping study involves an ergodic process. However, in a later article, we will see that this definition is problematic.
Examples of ergodicity.
Electrons in atoms and molecules
The Birkhoff and von Neumann proofs supported advances in quantum mechanical descriptions of molecular structures that have flourished since the 1930s. Schrodinger’s equation (1926),* which was independently developed for the special case of electron behavior in fields of atomic nuclei and other electrons, became part of a larger mathematical and statistical framework. This author’s Ph.D. thesis on electron coupling effects in the NH radical was on a firmer footing because of the ergodicity theorem, unbeknownst to me at the time.
*Schrodinger was challenged by the de Broglie hypothesis in that physicist’s 1925 Ph.D. thesis. The hypothesis, known as the de Broglie equation, stated that the wavelength of any moving particle was proportional to the inverse of its momentum. The proportionality constant is known as the Planck constant.
Gas in a sealed container
The pressure of gas in a sealed container at a constant temperature remains constant over time. To understand how this relates to ergodicity, recognize that pressure results from gas molecules hitting the walls of the container. The rate at which a molecule hits the wall is proportional to its velocity. At any given time, there is an average velocity for all the molecules in the container. That average determines the temperature.
Now consider one molecule. Over time, its velocity will change as it collides with other molecules, sometimes gaining energy from faster-moving particles and other times losing energy to slower-moving particles. Since the temperature of the system is held constant, the average velocity of all molecules must remain the same. Over a long period, this requires that any specific molecule’s velocity gains/losses must average zero. Thus, the long-term average velocity of any molecule is the same as the average of all molecules at any singular time. This system is ergodic.
An excellent elementary source for ergodicity is Dellanna, Luca, Ergodicity – Definitions, examples, and implications, as simple as possible, Second Edition, 2022, @DellAnnaLuca, Luca-dellanna.com, Amazon.com
Conclusion
This post has set the stage for the article next week focusing on complex systems. The analysis includes how the ergodicity of the coin-flipping process is confounded in practice. Also, we review some situations where the assumption of ergodicity has been abused. Finally, we will discuss how what we learned from flipping three coins impacts on practices in economic modeling.
Caption Image by Gerd Altmann from Pixabay.
Previous Articles in the Series
Part 1: The Gamblers’ Paradox.
… Lounsbury, John, “Adventures With 3 Coin Flips. Part 1: The Gamblers’ Paradox,” EconCurrents, May 21, 2023, https://econcurrents.com/2023/05/21/adventures-with-3-coin-flips-part-1-the-gamblers-paradox/
Part 2: Connecting the Micro to the Macro.
… Lounsbury, John, “Adventures With 3 Coin Flips. Part 2: Connecting the Micro to the Macro,” EconCurrents, May 28, 2023, https://econcurrents.com/2023/05/28/adventures-with-3-coin-flips-part-2-connecting-the-micro-to-the-macro/
Part 3: Possibilities vs. Realities.
… Lounsbury, John, “Adventures With 3 Coin Flips. Part 3: Possibilities vs. Realities,” EconCurrents, November 19, 2023, https://econcurrents.com/2023/11/19/adventures-with-3-coin-flips-part-3-possibilities-vs-realities/
Part 4: Learning to Count at an Advanced Age.
… Lounsbury, John, “Adventures With 3 Coin Flips. Part 4: Learning to Count at an Advanced Age,” EconCurrents, November 26, 2023, https://econcurrents.com/2023/11/26/adventures-with-3-coin-flips-part-4-learning-to-count-at-an-advanced-age/.
Part 5: Identifying and Counting Outcomes.
… Lounsbury, John, “Adventures with 3 Coin Flips. Part 5: Identifying and Counting Outcomes,” EconCurrents, December 3, 2023, https://econcurrents.com/2023/12/03/adventures-with-3-coin-flips-part-5-identifying-and-counting-outcomes/.
Part 6: Probabilities.
… Lounsbury, John, “Adventures With 3 Coin Flips. Part 6: Probabilities,” EconCurrents, December 17, 2023, https://econcurrents.com/2023/12/17/adventures-with-3-coin-flips-part-6-probabilities/.
