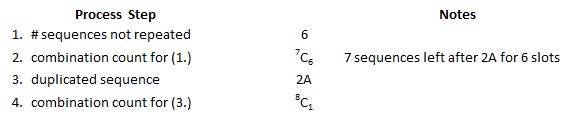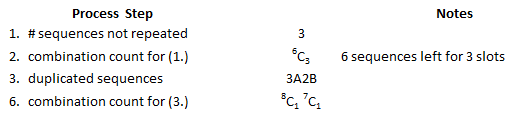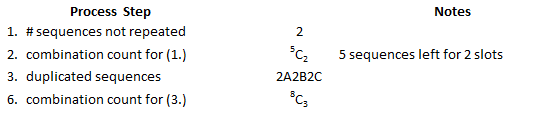This article describes the process of identifying all possible outcomes when there are 8 trials of 3 coin flips each. Then, the outcomes are divided into types, and the number of outcomes for each type is determined.
Types of Outcomes
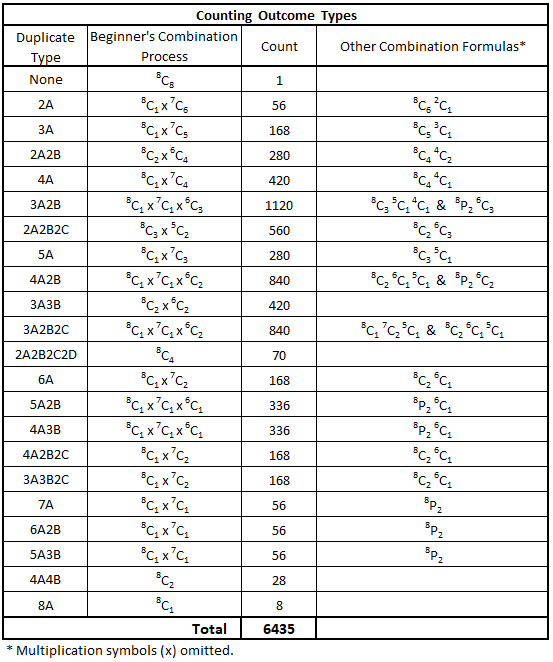
The table below shows the 22 outcome types for a trial of 8 successive 3 coin flips.
To interpret the above table, recall the definition of the eight 3-flip sequences from Part 4:
- HHH —> A
- HHT —> B
- HTH —> C
- HTT —> D
- THH —> E
- THT —> F
- TTH– -> G
- TTT —> H
The second thing to recognize is that the use of a letter (say, A) is symbolic. That means A can be replaced by any other letter B through H, and we have an outcome of the same type. For example, the Type 2 outcome is represented by AABCDEFG and is represented by the Duplicate Type 2A. The following list of outcomes are also members of Type 2A:
- 2B
- 2C
- 2D
- 2E
- 2F
- 2G
- 2H
Similarly, for Type 2A, the sequences BCDEFG are representatives for all combinations of 6 sequences that are not in 2X. In other words, these are all the combinations of 6 things that can be selected from a group of 7 objects.
A Further Example of Outcome Type
Consider Type 9: AABBCDEF, Duplicate Type 2A2B.
The duplicates (repeated sequences) 2A and 2B are symbolic representatives of all possible pairs of duplicates. Examples are 2F and 2H, 2D and 2H, 2G and 2C, 2E and 2A, etc.
The single sequences CDEF represent all possible combinations of four from the six sequences not in the two duplicates.
When the counting starts below, these examples will become clear and second nature. If not, you need to come back to the beginning and go through the definitions again.
Counting Outcomes
Initially, a consistent process of counting outcomes was difficult for me to achieve. After many trials, I learned how to count most outcome types in more than one way. But, to get started, I followed a reproducible process to get correct results consistently.
Counting Process for Beginners
The process I call the “Beginner’s Combination Process” has the following steps:
- Determine the single (not repeated) sequences in the outcome.
- Write down the combination count for those sequences.
- Next, look at the duplicate sequence(s).
- If there is only one sequence duplicated, write down the combination count for that sequence. Count it as a single entity regardless of the number of times it is duplicated.
- If there are 2 (or more) sequences duplicated and each is duplicated to the same extent (like 2A2B), count it as two (or more) entities selected at the same time.
- If there are 2 or more entities duplicated to a different extent (like 3A2B), count each duplicated sequence as an individual entity.
The above rules are rather obtuse upon the first examination. They are best clarified with examples.
Example 1 – Type 2A
The structure of this outcome is AABCDEFG. The steps of the Beginner’s Process are:
Example 2 – Type 2A2B
The structure of this outcome is AABBCDEF. The steps of the Beginner’s Process are: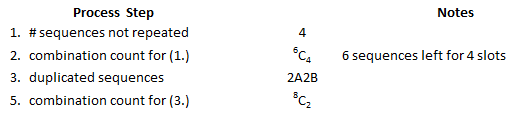
Example 3 – Type 3A2B
The structure of this outcome is AAABBCDE. The steps of the Beginner’ Process are:
Example 4 – Type 2A2B2C
The structure of this outcome is AABBCCDE. The steps of the Beginner’s Process are:
Example 5 – Type 2A2B2C2D
The structure of this outcome is AABBCCDD. The steps of the Beginner’s Process are:
Example 6 – Type 5A3B
The structure of this outcome is AAAAABBB. The steps of the Beginner’s Process are:
Outcomes for all 22 Types
Following the process outlined above, all 22 outcome types have been counted. We see the validity of the count is confirmed by the total for all outcomes, 6,435 – this was the number previously determined in Part 4.
Conclusion
We need to remind ourselves that we are dealing with a very simple process: flipping a coin three times. Understanding what all outcomes are for repeating that simple process just 8 times in order to have enough flips to allow each of the 8 possible sequences to be achieved has revealed astounding complexity. We started with the simple possibility table of 8 equally probable results for 3 coin flips. Part 2 of this series shows that what is possible at t(0) doesn’t represent what will happen at t(1), t(2), etc. Someone gambling on coin flips would be deceived by confusing reality and parallel universes.
The original possibility table can occur in reality. But this can only happen as one of 6,435 possible outcomes for the coin-flipping process.
Again, don’t forget this is a simple process: Flipping a coin 3 times. And the probabilities for every step in the process are clearly defined. What we have seen is much simpler than trying to model a system with unknown probabilities for elements in the system. Many models don’t reflect the exact process steps involved – they are often unknown and must be assumed.
The rabbit hole this coin-flipping process has taken us down is indeed complex, even though much simpler than many modeling situations. And it is about to get even deeper because we next consider what the probabilities are for each of the 6,435 outcomes.
Next Article: Part 6: Probabilities
Caption image: Image by _Alicja_ from Pixabay
Previous Articles in the Series
Part 1: The Gamblers’ Paradox.
… Lounsbury, John, “Adventures With 3 Coin Flips. Part 1: The Gamblers’ Paradox,” EconCurrents, May 21, 2023, https://econcurrents.com/2023/05/21/adventures-with-3-coin-flips-part-1-the-gamblers-paradox/
Part 2: Connecting the Micro to the Macro.
… Lounsbury, John, “Adventures With 3 Coin Flips. Part 2: Connecting the Micro to the Macro,” EconCurrents, May 28, 2023, https://econcurrents.com/2023/05/28/adventures-with-3-coin-flips-part-2-connecting-the-micro-to-the-macro/
Part 3: Possibilities vs. Realities.
… Lounsbury, John, “Adventures With 3 Coin Flips. Part 3: Possibilities vs. Realities,” EconCurrents, November 19, 2023, https://econcurrents.com/2023/11/19/adventures-with-3-coin-flips-part-3-possibilities-vs-realities/
Part 4: Learning to Count at an Advanced Age.
… Lounsbury, John, “Adventures With 3 Coin Flips. Part 4: Learning to Count at an Advanced Age,” EconCurrents, November 26, 2023, https://econcurrents.com/2023/11/26/adventures-with-3-coin-flips-part-4-learning-to-count-at-an-advanced-age/.