Adventures With 3 Coin Flips. Part 3: Possibilities vs. Realities

Flipping a coin three times seems like a simple process. But there are myriad complications that can arise. In Part 1 of this series, we saw that data sampling for coin flips can influence how results are interpreted. In this post, we will look closely at how probability assessments (possibilities) can lead to propositions deviating from the reality ensuing when coin flips are actually carried out. We will consider the concept of ‘alternate universes’. Who would have guessed that flipping a coin three times would go there?

Possibilities

In Part 1, we saw the array of possible outcomes for flipping a coin three times. Jason Collins and Blair Fix showed eight equally probable sequences:

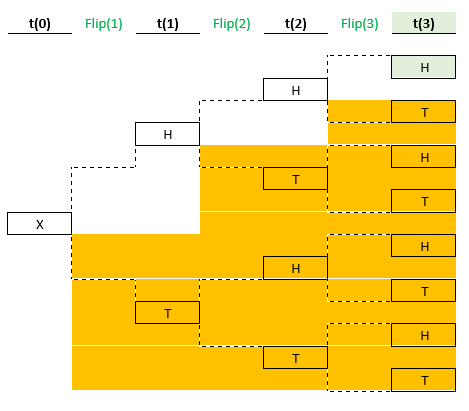
For this discussion, it is useful to display these in a flow diagram:

Let’s walk through this diagram.

Starting at t(0), we are waiting to flip the coin. At t(1), we have flipped the coin, and it is either H or T. The diagrams below show what happens when the first flip is H. After getting that first H, the bottom half of the ensemble in the diagram above is no longer available. At t(1), it has been determined that T is not possible at this point in this time sequence. Reality exists only for Heads at t(1).

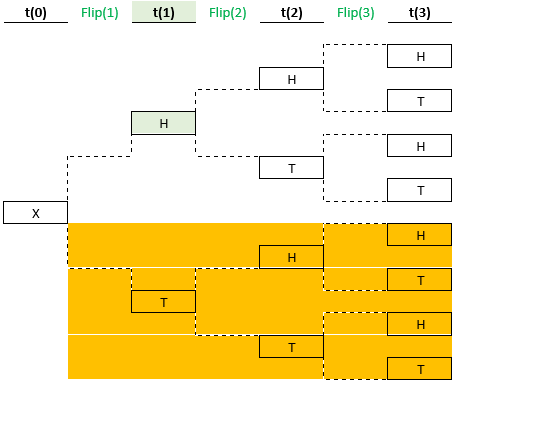
Reality

At time t(2), two possibilities remain available (and still two more are no longer available). If the second flip is Heads, the diagram becomes:

At time t(3), the result of Flip(3) is determined, and only one sequence remains. If Flip(3) produces Heads, the diagram becomes:

Only one of the eight possible sequences survives in reality. This will be the case for every sequence of three flips. Every time a coin is flipped three times, seven of the possible outcomes will not occur.

This is the nature of life. Every action, every decision, every choice eliminates things that might have been. It is starkly visible in the coin-flipping exercise because the probabilities of possible results are known before the first flip. In many situations in life, all possibilities at any point in time may not be recognized. And those that are recognized often do not have defined probabilities. As a result, many lost opportunities in life are not as readily analyzed as they are with coin-flipping.

Using a term from theoretical physics, the eliminated sequences exist only in a parallel universe. Who would have thought that flipping a coin three times would lead to considering parallel universes? This is indeed down a rabbit hole.

Complexity

Another aspect of reality arises with the probability table laid out by Fix. If one repeats the 3-flip sequence eight times, it is possible to obtain each one of the eight equally probable results. However, that is extremely unlikely. There are thousands of possible outcomes for the process. This is the topic explored in the next part of this series.

Summary

We are starting to see that flipping a coin three times is far from a simple process to analyze. It is easy for a gambler to confuse what is possible with what can actually occur. What one sees as odds before the flipping starts can lead to expectations that seem rational. But what is experienced with a series of 3-flip sequences can be much different from the rational expectations. We will come back to this conclusion at the end of the series when we discuss ergodicity.

Part 4: Learning to Count at an Advanced Age.

Caption graphic credit: Image by Gerd Altmann from Pixabay.

Previous Articles in this Series

Part 1: The Gamblers’ Paradox.
… Lounsbury, John, “Adventures With 3 Coin Flips. Part 1: The Gamblers’ Paradox,” EconCurrents, May 21, 2023, https://econcurrents.com/2023/05/21/adventures-with-3-coin-flips-part-1-the-gamblers-paradox/

Part 2: Connecting the Micro to the Macro.
… Lounsbury, John, “Adventures With 3 Coin Flips. Part 2: Connecting the Micro to the Macro,” EconCurrents, May 28, 2023, https://econcurrents.com/2023/05/28/adventures-with-3-coin-flips-part-2-connecting-the-micro-to-the-macro/