Adventures With 3 Coin Flips. Part 4: Learning to Count at an Advanced Age

The process of understanding the complexity of many 3-flip sequences for tossing a coin is about to become more difficult.  This is because are going to enter the arcane world of permutations and combinations.  As a result, this is counting on a scale far more complex than that learned in elementary school.

Counting Results for Multiple Coin Flips

As we have seen previously, there are 8 equally probable possible results for the 3-flip sequence.  The general formula for the number of possible results for a series of events when each event has the same number of possible outcomes is n^r.  In this, n is the number of possible results for each event and r is the number of events in the series.  Thus, for a 3-times repetition of an event with a binary result, the number of possible results is 2³. The attractiveness of using a 3-flip sequence rather than 4, 5, 6, or more is the rapid increase in possible results to be considered. Each flip added doubles the number of results possible.  By the time one gets to 6 flips the number of possible results is 64.

Below, we identify each equally probable sequence with a letter identifier:

1. HHH —> A
2. HHT —> B
3. HTH —> C
4. HTT —> D
5. THH —> E
6. THT —> F
7. TTH —> G
8. TTT —> H

If one wants to calculate the results for several 3-flip sequences, the problem becomes one of determining all the combinations and permutations possible for the 8 sequences.

With one 3-flip sequence, the possible results are 8 in number: A, B, C, D, E, F, G, or H

The number of possible results for repeating the 3-flip sequence a second time is straightforward.  All the combinations possible for the 8 results for two 3-flip sequences are equal to 28 if no repetitions are allowed, and 36 if repetitions are allowed.

This diagram technique can get confusing as the number of things to be selected increases above two.  So, let’s go back and start at the beginning.

Definitions for Coin Flips

First, we will define terms.

• Event – a single coin flip.
• Sequence – 3 coin flips.
• Outcome – the result of eight 3 coin flip sequences.

The reason for selecting 8 sequences: That is the minimum number that allows each of the sequences, A through H, to occur once.  This allows for all the possible combinations of the eight sequences to be counted.

Definitions for Counting

When we carry out 8 sequences of 3 coin flips, we want to know how many outcomes are possible.  We have already seen previously the outcome where each one of the possible sequences occurs once.  That outcome is ABCDEFGH.

But there are many more possible outcomes.  The number is found using a formula for the number of combinations with repetitions allowed.  Any of the 8 sequences can occur in any 8 “boxes” in an outcome.  This means that if A was the first outcome, A is just as likely to be the second outcome as any of the 7 others B, C, … H.

From Discrete Math, Zheijiang University, Spring 2013, with Greg Baker, we have a summary table for how to calculate ways to select r things from n possibilities:

In this series of posts, we use the following notation for the counting of outcomes:

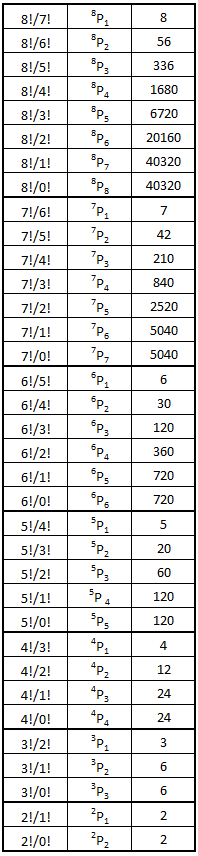
P(n,r) = n!/(n−r)! = ⁿP_r

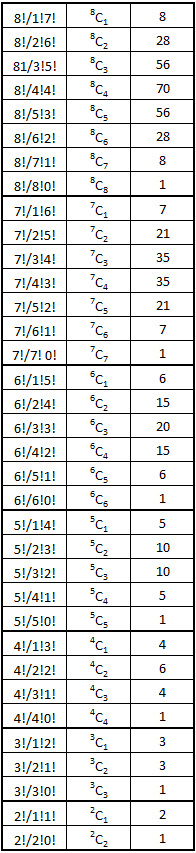
C(n,r) = n!/r!(n−r)! = ⁿC_r

Number of Possible Combinations of A, B, …, H

In our coin-flipping exercise, we will select possible combinations of 8 things from 8 objects with replacement.  The total number of outcomes is 6,435, calculated as follows:

C (n+r-1,r) = (n+r−1)!/r!(n−1)! =

(8+8−1)!/8!(8−1)! =

15!/8!7! =

15 x 14 x 13 x 12 x 11 x 10 x9/7! = 6435

We can see the consideration of only the single possibility ABCDEFGH previously was a significant oversimplification.  There are 6,434 additional possible outcomes.

Combinations

In characterizing each of the 6,435 outcomes, we will be counting a variety of combinations.  These will be defined in the next article in this series.  The values for those combinations are included in the following table of all combinations possible for arrays of elements up to 8 in number.  This table is constructed without repetition. This is because when we count in the next post of this series, repeated sequences will be counted as one element.

Permutations

It is possible to count and identify all 6,435 possible outcomes for 8 trials of 3 coin flips each.  But there will be a few situations where the counting can also include permutations in an alternative process to all combinations only.  Also, when we consider all possible pathways to produce each combination, permutations will be used.  So, we have calculated the values for permutations of all possible elements in arrays of up to 8 elements.  As for combinations, the permutations are determined without repetition. This is because when we count in the next posts of this series, repeated sequences will be counted as one element.

Conclusion

We now have covered all the background of counting operations.  In the next post, we identify all possible outcomes and do the actual counting.

Next article:

Part 5:  Identifying and Counting the Outcomes

Previous Articles in this Series

Part 1: The Gamblers’ Paradox.
…  Lounsbury, John, “Adventures With 3 Coin Flips. Part 1: The Gamblers’ Paradox,” EconCurrents, May 21, 2023, https://econcurrents.com/2023/05/21/adventures-with-3-coin-flips-part-1-the-gamblers-paradox/

Part 2: Connecting the Micro to the Macro.
…  Lounsbury, John, “Adventures With 3 Coin Flips. Part 2: Connecting the Micro to the Macro,” EconCurrents, May 28, 2023, https://econcurrents.com/2023/05/28/adventures-with-3-coin-flips-part-2-connecting-the-micro-to-the-macro/

Part 3: Possibilities vs. Realities.
… Lounsbury, John, “Adventures With 3 Coin Flips. Part 3: Possibilities vs. Realities,” EconCurrents, November 19, 2023, https://econcurrents.com/2023/11/19/adventures-with-3-coin-flips-part-3-possibilities-vs-realities/