Federal Deficit Spending (Quarterly) and Inflation. Part 4

This article concludes the analysis of the correlation patterns between quarterly Federal Deficit Spending (FDS) and Consumer Inflation (CPI).  The last of the three types of inflation patterns (time periods with no significant inflation trends) is the subject of analysis here.  The other two types of patterns (inflation surges¹ and disinflation/deflation surges²) were analyzed previously.  The conclusion discusses the correlation patterns for all time periods, looks for any common threads, and identifies important differences across time periods and types of correlation patterns.

From photo by Live Richer on Unsplash.

Introduction

The hypothesis we are testing is that inflation depends on nonfinancial corporate credit in a linear manner, expressed in the following equation:³

I = mS + b

where

I = Change in CPI (the Consumer Price Index)

S = Change in Federal Deficit Spending

Data

The data sources³ and tables for FDS and CPI are in Part 1.  The timelines³ for the two data sets in Part 1 have coincident timelines and offsets by three and six months out to 24 months for FDS coming before CPI and vice versa.

The inflation timeline from 1952 through 2022 uses year-over-year inflation calculated quarterly.  Figure 1 shows the inflation graph for the 1952-2022 time period (from Part 1).

Figure 1.  CPI Rolling Four Quarter Inflation 1952-2022 with Significant Changes in Inflation Noted
(Each letter identifies the end of a significant move.  An * identifies the end of an insignificant time period.)

Table 1 shows the data from Figure 1.

Table 1.  Timeline of Inflation Data 1952-2022 (Previously Table 4*.¹)

In Table 1, a black letter identifies a significant positive surge in inflation, a red letter for significant negative surges, and no letter for time periods with no significant changes in inflation.

Significant surges are changes in inflation ≥4% with no intervening countertrend moves >1.5%.

Analysis

There are 13 quarterly timeline alignments examined in each of the 5 time periods:

• FDS and CPI Inflation quarters are coincident.
• FDS leads and lags CPI Inflation by one quarter (±3 months)
• FDS leads and lags CPI Inflation by two quarters (±6 months)
• FDS leads and lags CPI Inflation by three quarters (±9 months)
• FDS leads and lags CPI Inflation by four quarters (±12 months)
• FDS leads and lags CPI Inflation by six quarters (±18 months)
• FDS leads and lags CPI Inflation by eight quarters (±24 months)

There are four time periods with no inflationary or deflationary surges between 1966 and 2022, the years for which quarterly federal government deficit spending data is available.

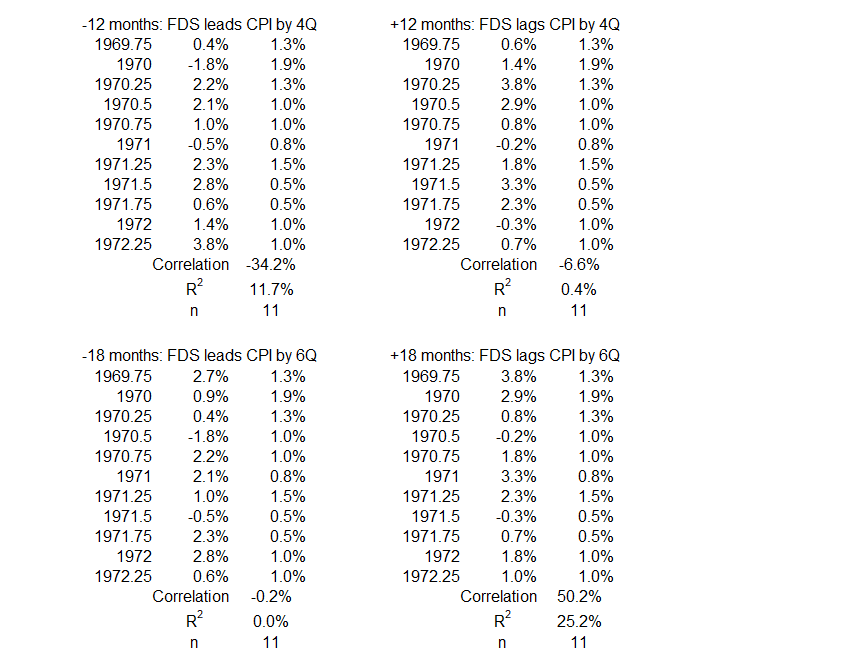
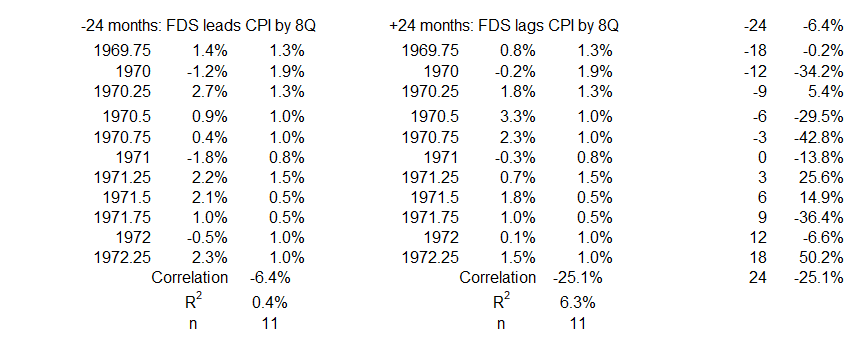
1Q 1970 – 2Q 1972

Figure 2. U.S. FDS and Inflation 4Q 1969 – 2Q 1972

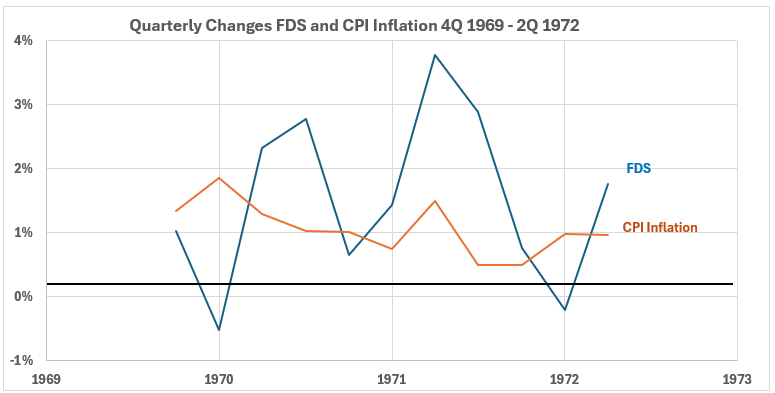
In this period, inflation changes are relatively stable in a downward trend.  FDS changes are in an uptrend for six quarters and then in a downtrend for four.  The volatility of the FDS changes is much greater than for CPI.

Figure 3.  Quarterly Changes in FDS (x) vs. CPI Inflation (y) 4Q 1969 – 2Q 1972

The association (correlation) between FDS and CPI Inflation with concurrent timelines is very weakly negative during this relatively stable inflation period:  R = –13.8%, R² = 1.9%.

Figure 4.  Correlation Between FDS and CPI Inflation 4Q 1969 – 2Q 1972

Figure 4 shows the positive association of FDS changes with inflation changes is weakly negative (R = –43%, R² = 18%) when credit comes before inflation by three months (left side of the graph).  For all other data points on the left, FDS changes are more weakly or negligibly correlated with later inflation changes.  There is the possibility that changes in FDS might contribute up to 18% of changes in inflation in the opposite direction.  Importantly, the data shows that there was no contribution of federal deficit spending to increases in inflation during this period.

On the right side, the data point for inflation changes coming 18 months before FDS changes indicates the possibility that CPI changes might result in FDS changes. R = 50% and R² = 25% allow for the possibility that changes in CPI might contribute up to 25% of changes in FDS in the same direction.  However, no other data points come close to supporting the 18-month offset.  Note that causation cannot be confirmed or eliminated without additional information.

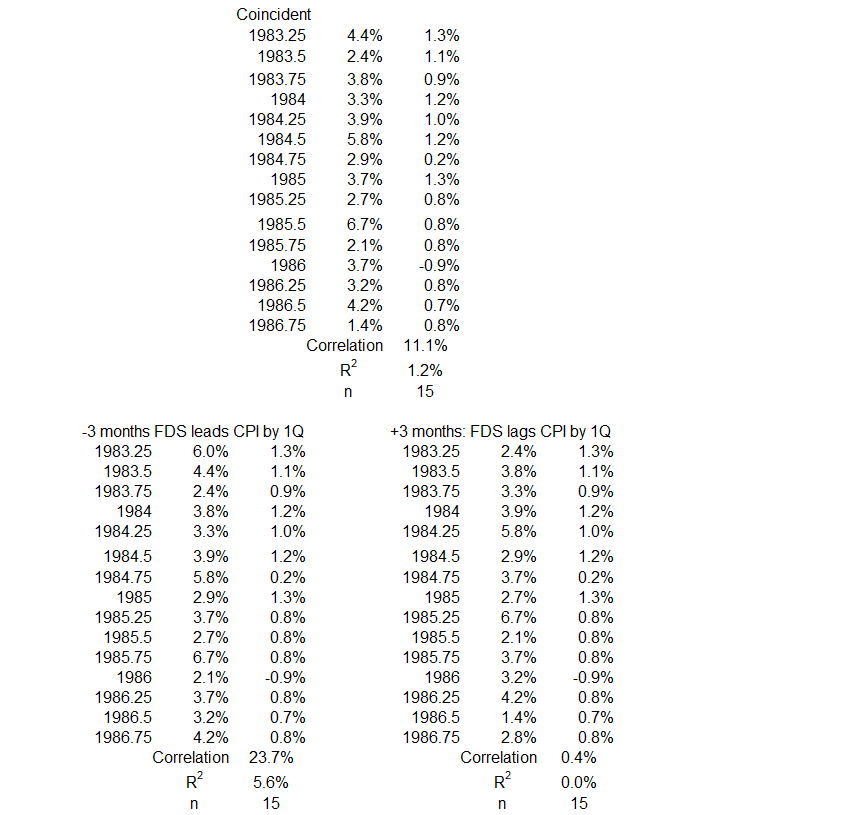
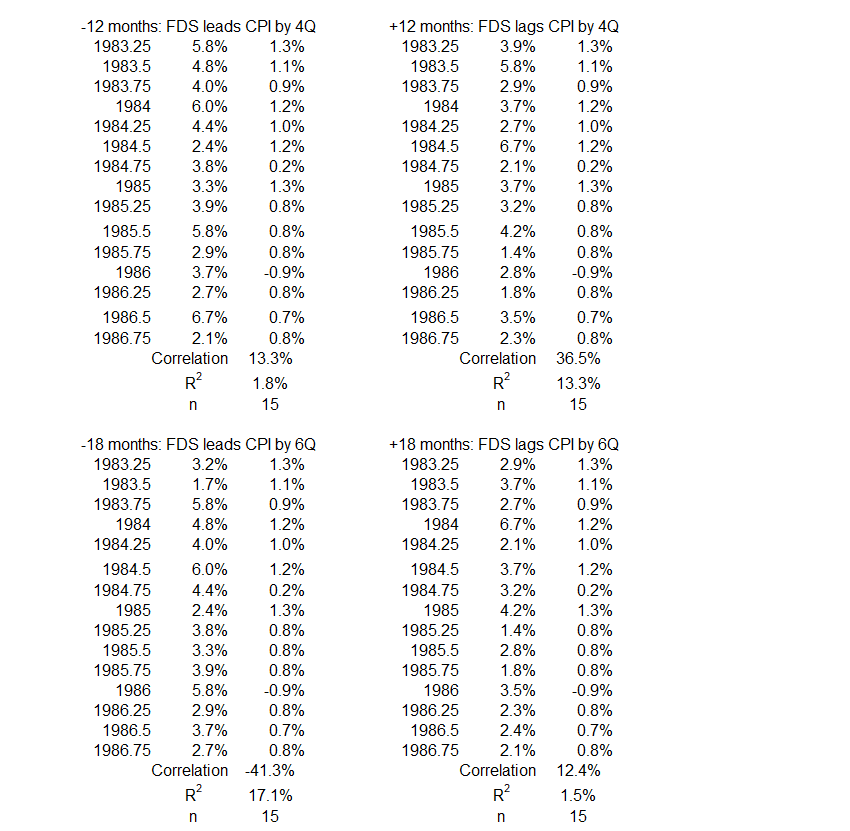
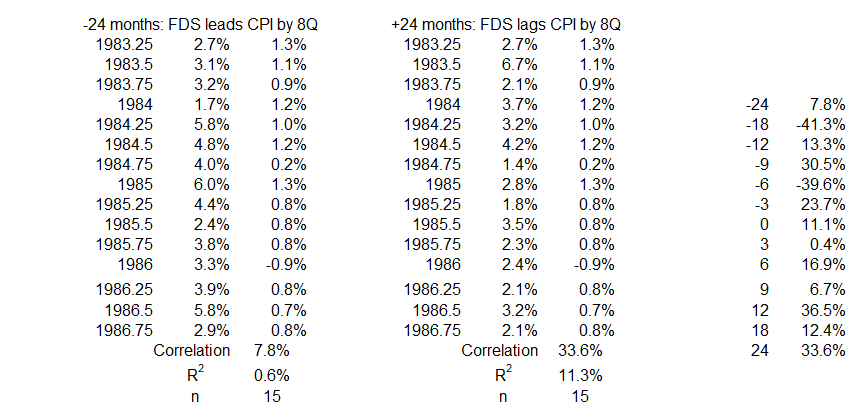
3Q 1983 – 4Q 1986

Figure 5. U.S. FDS and Inflation 2Q 1983 – 4Q 1986

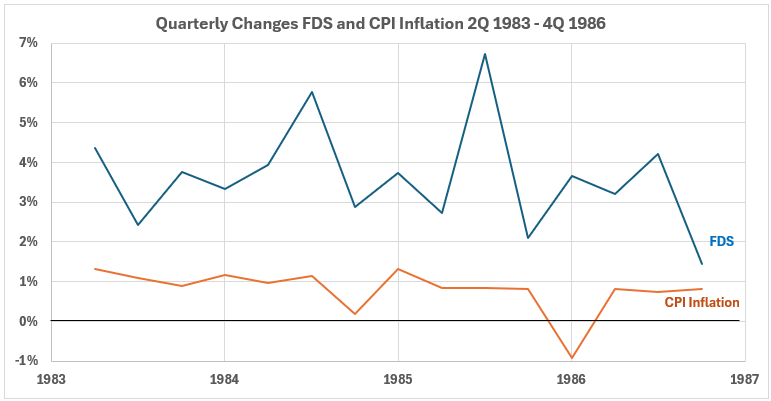
Figure 5 shows slight down-trending quarterly changes for CPI, with one deflationary dip for the first quarter of 1986.  The quarterly changes for FDS show a nearly level trend.  The much larger volatility for FDS changes has moderated here from that seen in the 1970-72 period.

Figure 6.  Quarterly Changes in FDS (x) vs. CPI Inflation (y) 2Q 1983 – 4Q 1986

This period shows a slightly positive correlation:  R = 11%, R² = 1.2% for the coincident timelines data.

Figure 7.  Correlation Between FDS and CPI Inflation 3Q 1983 – 4Q 1986

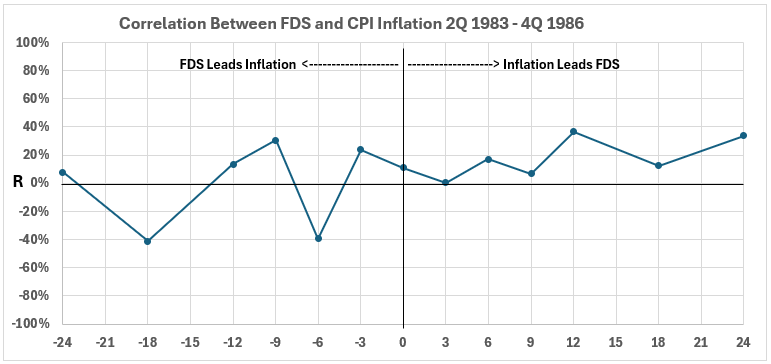
On the left side of the graph, there are weak negative associations, both positive and negative. The two negative correlations (-6 and -18 months) are near R = 40% (R² = 16%). This means that up to 16% of changes in inflation might have been caused by changes in FDS in the opposite direction. The largest positive association at -9 months has R = 30% and R² = 9%.  That indicates that increases in inflation were at least 91% caused by factors other than federal deficit spending.  The same statement can be made for decreases in the two variables.

On the right side of the graph, there is little that is remarkable.  The data point for 12 months offset of timelines, R = 37% and R² = 13%, indicates that at least 87% of the changes in FDS must be caused by factors other than changes in inflation.

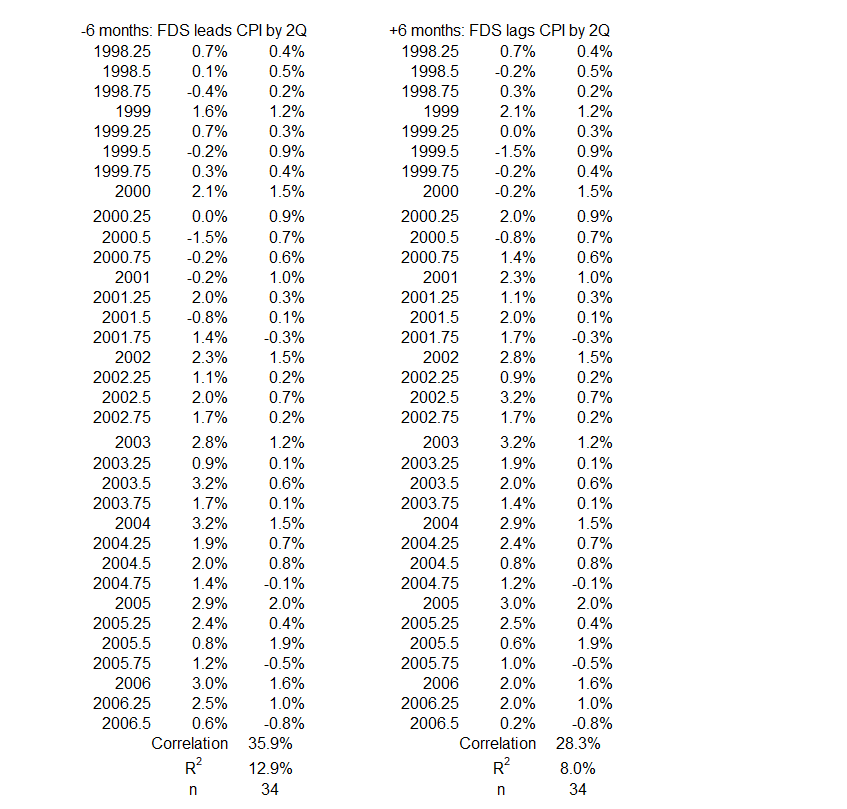
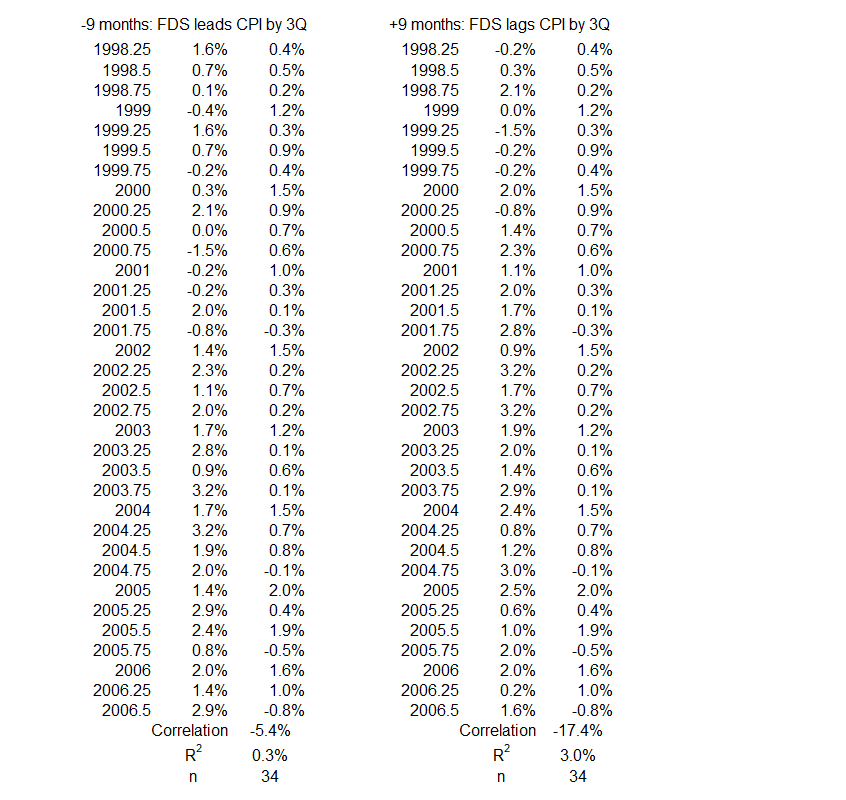
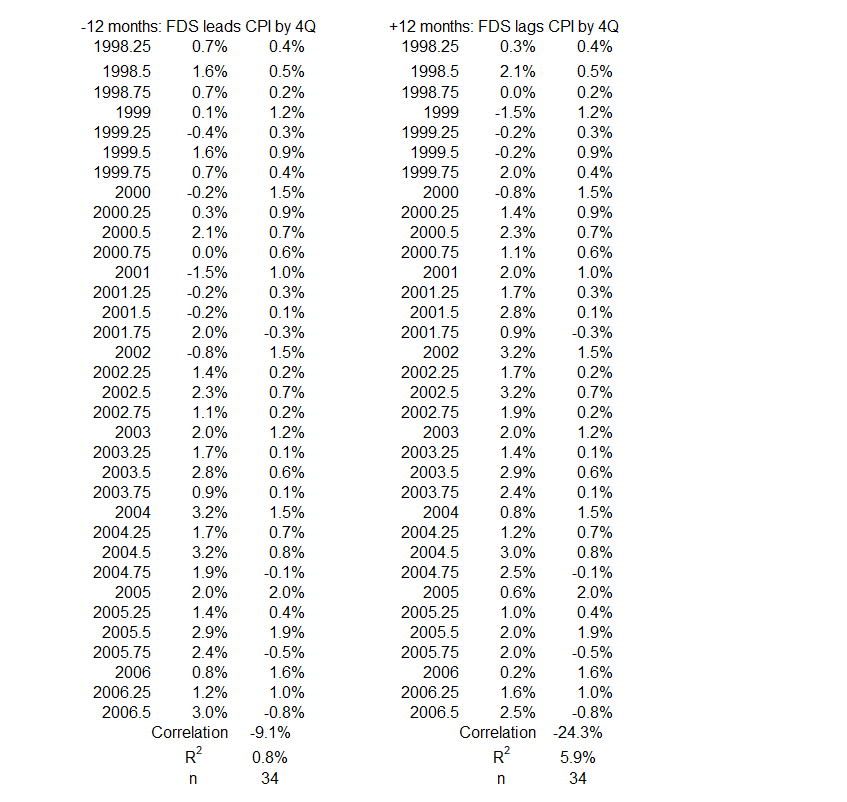
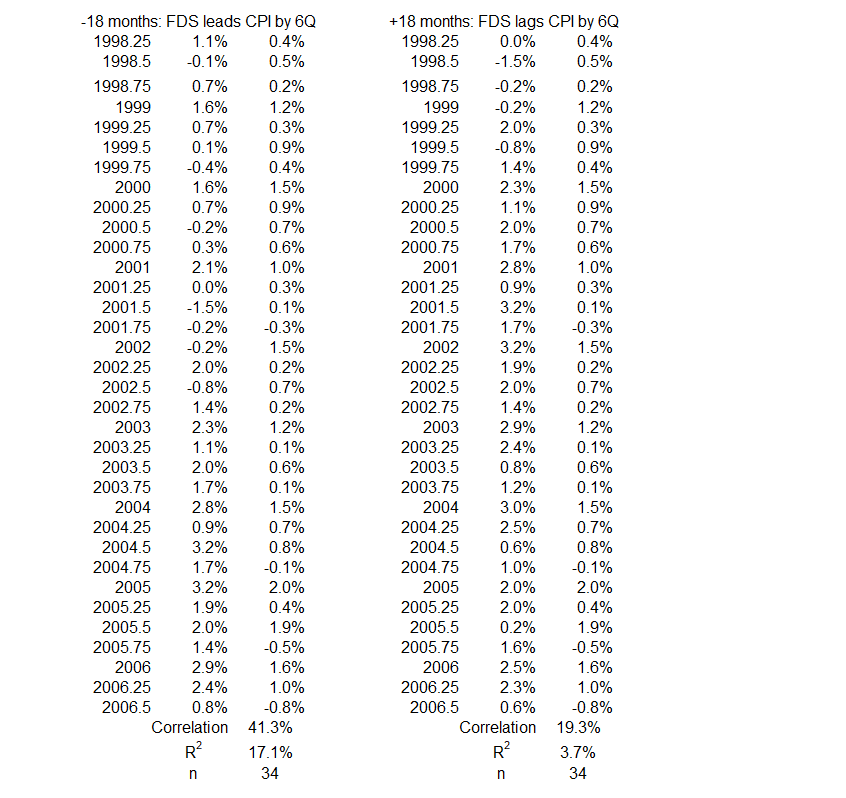
2Q 1998 – 3Q 2006

Figure 8. U.S. FDS and Inflation 2Q 1998 – 3Q 2006

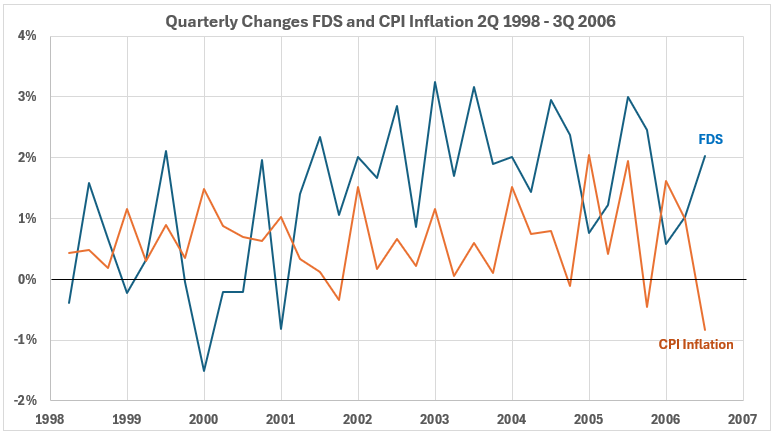
Figure 8 shows a level trend for CPI changes and a slight uptrend for FDS changes.  The volatilities in the two variables are more similar here than seen previously.

Figure 9.  Quarterly Changes in FDS (x) vs. CPI Inflation (y) 2Q 1998 – 3Q 2006

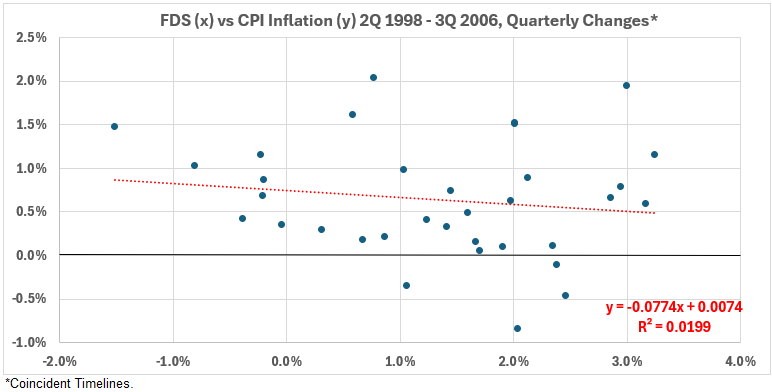
This data shows a small negative correlation for coincident timelines data:  R = –14%, R² = 2%.  This association can be considered negligible.  It indicates that at least 98% of the quarterly variation in FDS is not caused by coincident CPI inflation or vice versa.

Figure 10.  Correlation Between FDS and CPI Inflation 2Q 1998 – 3Q 2006

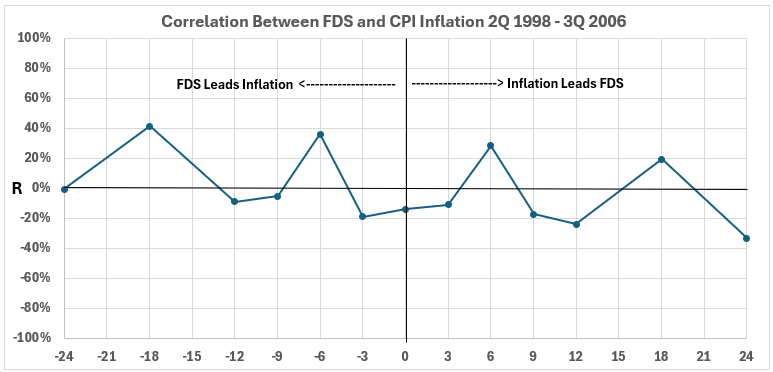
Figure 10 indicates that there is a limited association between FDS and CPI inflation for this 102-month period.  The highest value of R is 41% for any of the data pairs.  That produces an R² = 17%, the maximum amount of change in one variable possibly caused by a change in the other.  In other words, more than 83% of the change in either of these variables has to be caused by something besides the other variable during this period.

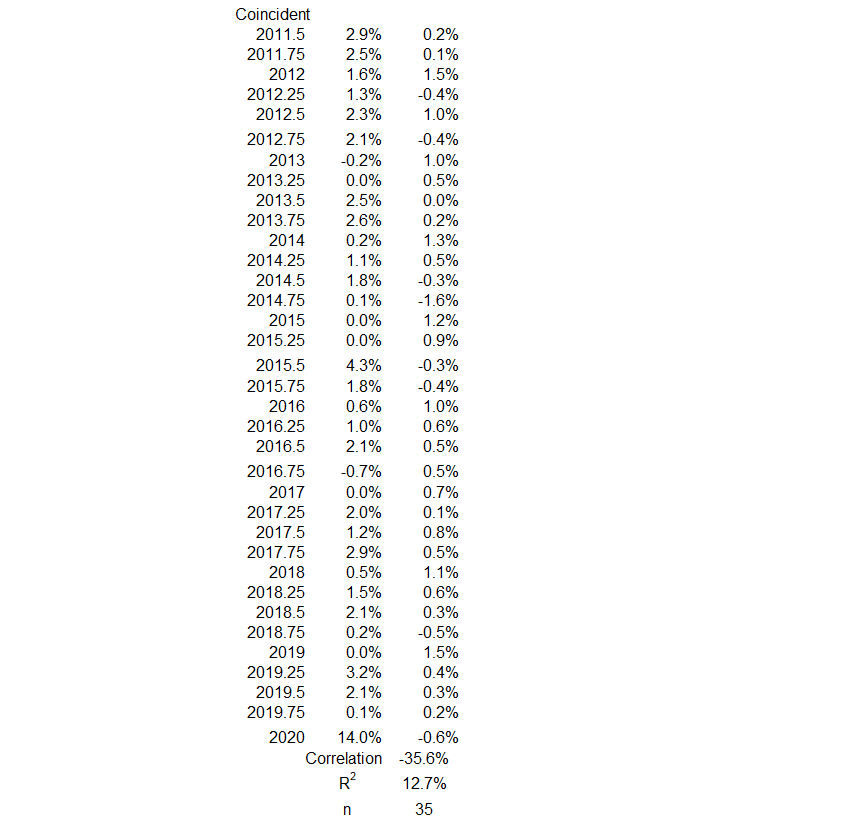
3Q 2011 – 1Q 2020

Figure 11. U.S. FSD and Inflation 3Q 2011 – 1Q 2020

Figure 11 shows quarterly CPI inflation and FDS changes are both generally in level trends.  The remarkable points in this graph are three:

1. There are seven deflationary quarters.
2. There are three quarterly contractions in FDS and three quarters with nearly zero change.
3. There are two noteworthy spikes in FDS – in the second quarter of 2015 and especially in the first quarter of 2020.

Figure 12.  Quarterly Changes in FDS (x) vs. CPI Inflation (y)  3Q 2011 – 1Q 2020

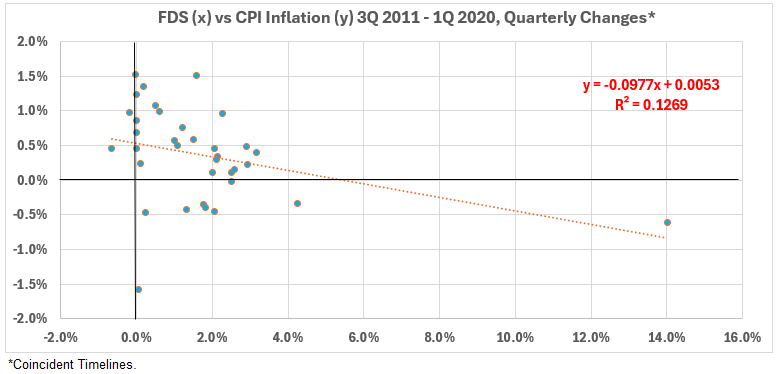
The coincident timeline data show a weak negative correlation in this time period: R = –36%, R² = 13%.

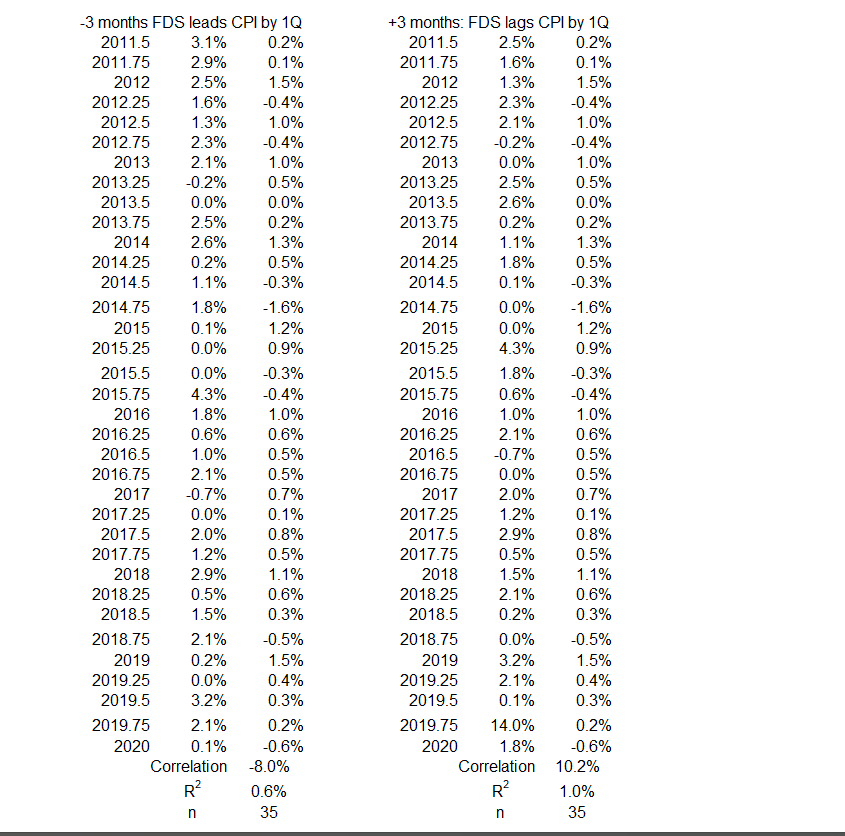
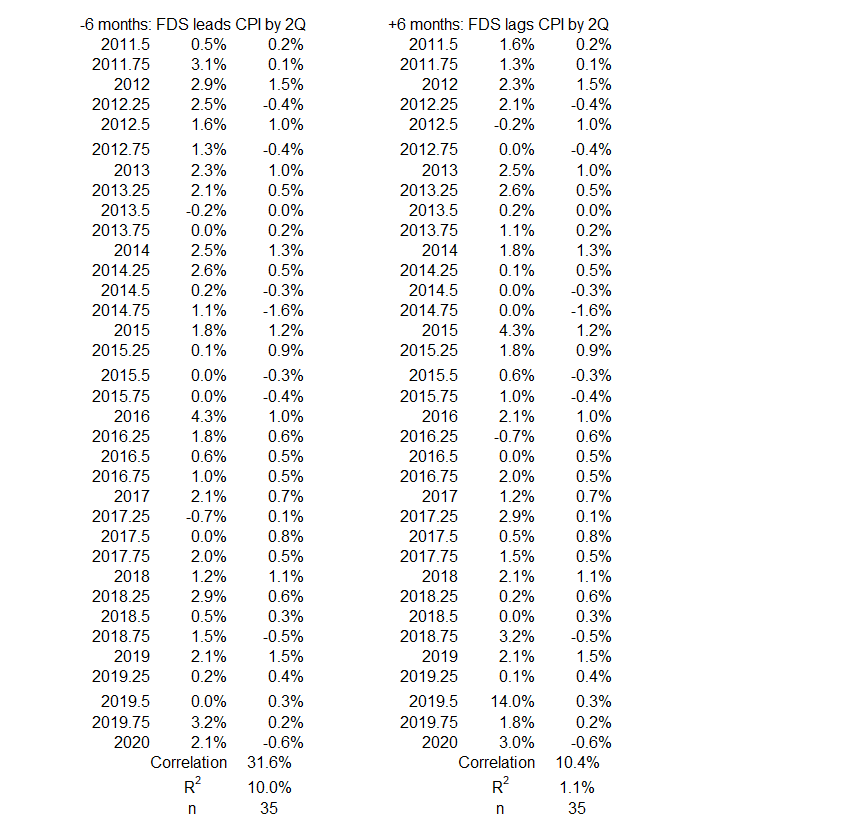
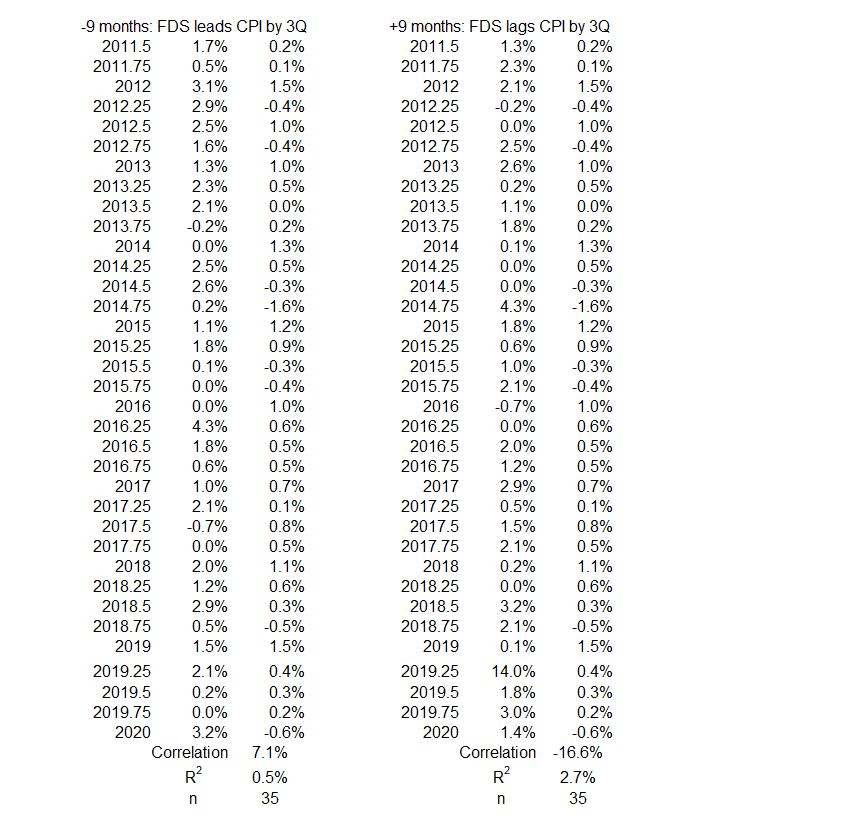
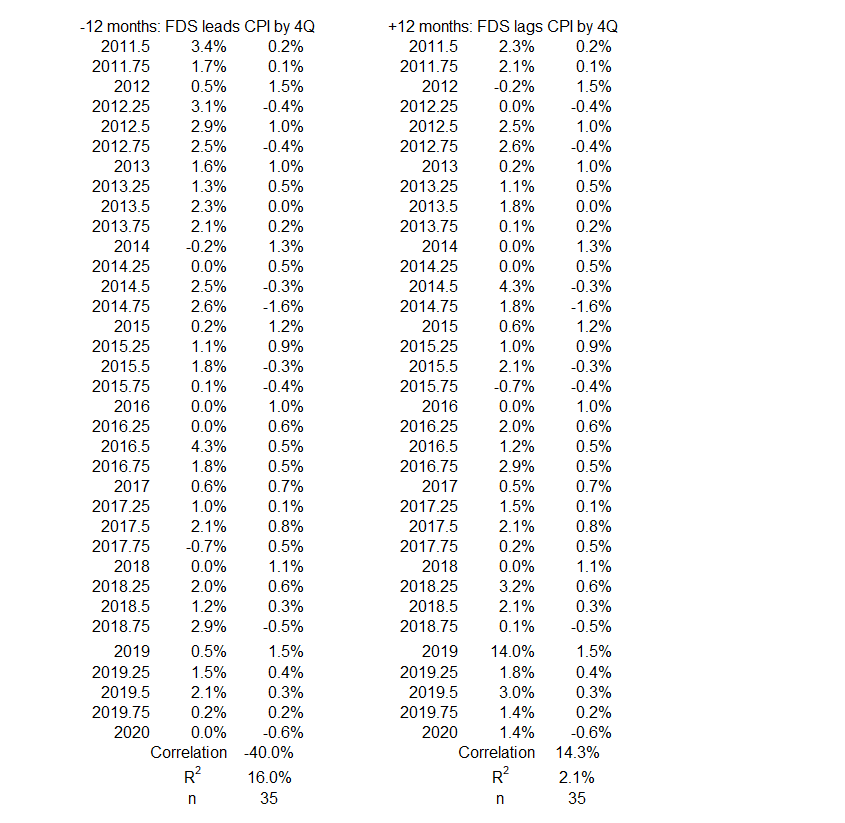
Figure 13.  Correlation Between FDS and CPI Inflation  3Q 2011 – 1Q 2020

There is little opportunity for either variable to have possibly caused a significant or moderate change in the other.  On the left side, at least 84% of the change in inflation is caused by something other than an opposite change in FDS (-12 months, R = –40%, R² = 16%).  At least 90% of the change in inflation is caused by something other than a change in FDS in the same direction (-6 months, R = 32%, R² = 10%).

On the right side, at least 97% of the change in FDS is caused by something other than a change in CPI inflation.

Conclusion

The conclusion is divided into two sections. First, the analysis results are discussed for the current study of time periods without significant inflation surges up or down. Then, there is an overall summary of associations between FDS and CPI for inflation/disinflation periods and a look forward to future work.

Patterns of Correlation for Periods without Significant Inflation Surges

To simplify this discussion, the five periods without significant surges in inflation are numbered, as shown in Table 2.

Table 2. Time Periods with No Inflation/Disinflation Surges 1966-2022

There are fewer correlations found in this data than those for other money growth change sources.  The general observations for the five periods analyzed in this article are:

• Inflation volatility quarter-to-quarter is less for II and III compared to IV and V.

• There are no moderate positive or negative associations between FSD changes and subsequent inflation changes.

• One borderline moderate positive association occurred for inflation changes and subsequent FSD changes (II).

Overview of All Financial Sector Debt Spending Data Sets

Let’s review the results for all 15 time periods – positive and negative inflation surges plus the periods without surges analyzed above.  We use the letter designations in Table 1 and the numerical designations in Table 2 to simplify the discussion.

Table 3 summarizes the results for all time periods for correlation (association) of quarterly FDS changes with CPI Inflation changes.  In the table, black letters are for periods with positive inflation surges, red letters are for periods with negative inflation surges, and Roman numerals are for periods without surges.

Table 3. Associations Between Quarterly FDS and CPI Inflation 1966-2022

The associations shown in Table 3 indicate the maximum possible cause-and-effect relationships.  Significant association indicates R²>50%.

The moderate correlation strength covers the range 50%>R²>25%.  So, for example, R² = 40%, no more than 40% of one variable can result from the other.  However, the lower limit of cause-and-effect is zero, depending on other information in addition to the statistical result.  As stated differently, the cause of one variable is between 60% and 100%, based on factors other than the second variable.

The weak and negligible associations give a more satisfying result.  They indicate that much (more than 75%) of the cause of one variable comes from other sources than the second (weak association), or nearly 100% comes from other sources (negligible).

There are a few possibilities for more than 50% cause-and-effect (significant strength), but the proof is not given without further information.

There are also some possibilities for important cause-and-effect relationships between 25% and 50% (moderate strength).  However, additional information is needed in each case to prove that the causations are not lower than R² would indicate.

The most remarkable feature of Table 3 is that the number of events in the weak and negligible classes is much greater than in the moderate and significant classes.  This is more pronounced than for most other sources of money we have studied.

Summary

Next, we will compare the quarterly Federal Deficit Spending results discussed above with the annual FDS results provided previously using fiscal year deficit data.⁵

Appendix

Below are the data sets for each period without surging inflation or disinflation/deflation. They come from the tables of timeline alignments³ (Federal Deficit Spending (Quarterly) and Inflation: Part 1).

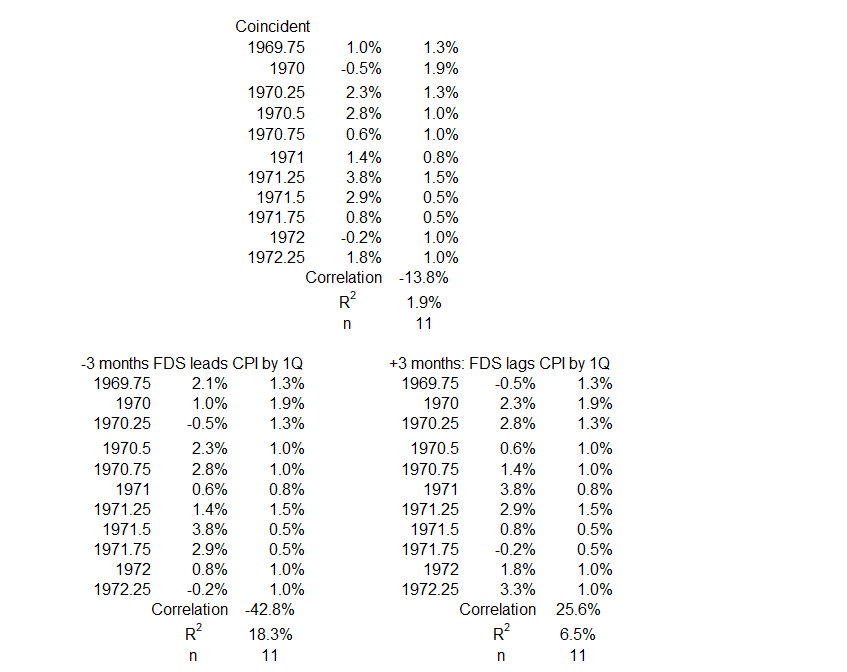
3Q 1983 – 4Q 1986

3Q 2011 – 1Q 2020