
This is an article about the ability to predict peak snow and snow water content (SWE) accumulation early in the season. This can be helpful to water planners. I came across this in a webinar that had four excellent presentations and one was related to this article. Here is the link to the recording of that presentation. You may want to watch and listen to the recording of that webinar. The overall conclusion is that predictability from early-season snowfall is greatest where it is coldest which usually means high latitudes. That is not surprising but some may find the methodology of quantifying the degree of predictability to be interesting. A lot of detail is provided for the U.S. West but Figure 2 shows it is true across North America.
Abstract
SNOwpack TELemetry observations and model simulations both demonstrate that the fractional contribution of October through December (early season) snowfall to peak snow accumulation in North America increases with latitude due to both colder temperatures and Pacific storm tracks focusing further north earlier in the season. Early season snowfall also makes up greater than 60 percent of peak accumulation in interior low-precipitation locations leeward of mountains, particularly those that are subject to strong, warm winds and midwinter snow loss. Early season snow observations show promise in predicting peak snow water equivalent in locations where large-scale ocean-atmosphere patterns similarly influence fall and winter conditions, and in northern maritime locations where winter temperatures are warm enough that rain on snow and midwinter melt occur. Because climate change is likely to increase the extent of midwinter melt, the latter relationship is expected to become important over more locations in the future.
Key Points
- Fall snow contributes more to peak snow at colder and more northerly locations
- Fall snow can be used to predict peak snow where large scale ocean and atmosphere patterns influence annual snowfall variations
- Fall snow regulates cold content, which in warm regions may tip a snowpack between lasting or ablating midwinter, influencing peak snow
Plain Language Summary
Across North America, snow accumulates from October until the following spring. Early season snow, defined as the snow that accumulates by the end of December, is a greater fraction of total snow accumulation at higher latitudes and at colder locations. Early season snow accumulation can be used to predict peak snow accumulation. Predictions are more skillful at locations where fall precipitation is correlated with winter precipitation because more snow at the end of December indicates that weather patterns are favorable for greater than average snowfall to continue. Predictions also have skill at warmer northern locations where more snow on the ground early season increases the likelihood that mixed rain-snow events add water to the snowpack rather than melting the snow. Predictions at warm southern locations do not have skill because winter and spring snowfall is highly variable, and frequently little to no snow has accumulated by the end of December.
Some may need to click on “Read Here” to access the rest of this article.
1 Introduction
Northern Hemisphere snow falling in October, November and December has a large effect on soil temperatures and permafrost (Slater et al., 2017), on wildlife (Cosgrove et al., 2021), and on northern hemisphere circulation patterns (Henderson et al., 2018). Across the western continental United States, precipitation falls primarily in the fall and winter, making snow accumulation critical for predicting spring and summer streamflow, wildfire risks, and water supplies. Thus, seasonal snow predictability is of value for agriculture (Kapnick et al., 2018), hydropower (Hamilton et al., 2020), and resource management (Morelli et al., 2016).
Much work has gone into seasonal prediction of snow, ranging from physically based modeling (Kapnick et al., 2018) to correlations with atmospheric and sea surface temperature indices (McCabe & Dettinger, 2002). However, early season snow itself has been overlooked as a predictor. Early season snow variation results from local temperature and precipitation anomalies driven by large-scale ocean and atmospheric states and interactions between them, giving an indication of whether conditions are favorable for snow. Early season snow also represents the state of the land surface. At locations with seasonal, as opposed to intermittent, snow cover, snowfall is likely to remain on the ground until spring, meaning that spring snow on the ground will likely be as much as, if not greater than, fall snow. Early season snow accumulation may also influence the amount of additional snow to be accumulated. For example, snow cover extent over Siberia in November influences December sea level pressure patterns across the Arctic (Gastineau et al., 2017), which influence weather patterns and subsequent snowfall across the Arctic. Also, total snow on the ground predicts a snowpack’s cold content (Jennings et al., 2018), such that a deeper snowpack increases the capacity of the snowpack to retain mixed-phase precipitation, and a deeper snowpack is less subject to midwinter melt than a shallower snowpack.
Here, we use model simulations (Kim et al., 2021) and SNOwpack TELemetry (SNOTEL) observations (Schaefer & Paetzold, 2001) in western North America to investigate the following.
- On average, what is the relative ratio of early season snow to peak seasonal snow?
- In terms of interannual variability, how well does early season snow on the ground predict peak snow accumulation for the year?
- What factors explain spatial variations in the predictive skill of early season snow?
2 Data and Methods
2.1 Methodology
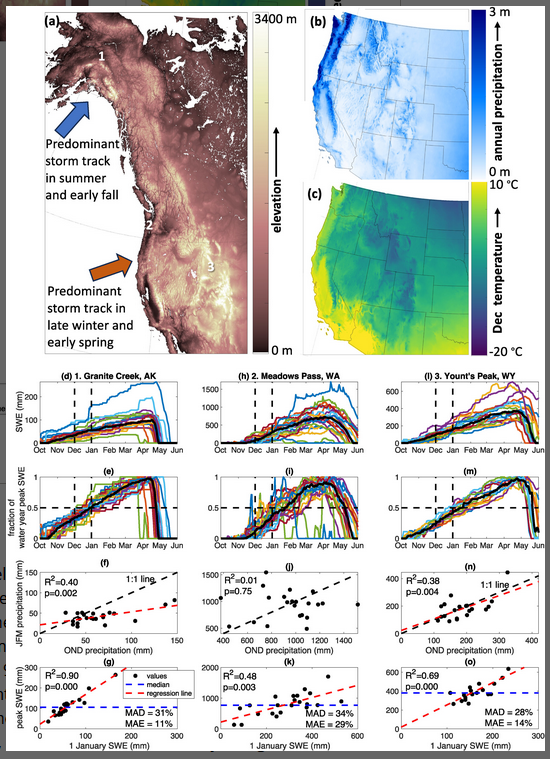
A water year is defined as 1 October of the prior year to 30 September. Early season snow is defined as the snow water equivalent (SWE) that accumulates on the ground by 1 December or by 1 January in the water year. This is compared with peak SWE accumulation at each site, which varies between January and May, depending upon site location and year (Kapnick & Hall, 2010).
2.2 Model Simulations
For continuous spatial coverage of North America, we used the entire duration (water years 2009-2017) of 5-km resolution simulations from the Snow Ensemble Uncertainty Project, SEUP (Kim et al., 2021), described further in Supporting Information S1. Of their multiple ensemble members, we chose to focus on the Noah-MP version 3.6 (Niu et al., 2011; Yang et al., 2011) snow simulations forced by Modern-Era Retrospective analysis for Research and Applications, MERRA-2 (Gelaro et al., 2017; Molod et al., 2015). Noah-MP is the most sophisticated of the models in the ensemble, representing 3 snow layers, the full energy balance, and influences of topography and forest cover on snow at a 5 km scale. MERRA-2 is globally available and widely used. Due to the snow model’s resolution, we expect it to capture large-scale patterns and timing well but not to match point observations of mountain snowpack. Thus, we use the model to complement the direct observations, providing continuous estimates of snow patterns at the full continental scale.
To answer question 1, for each pixel, we identified median values over the 9-year period of 1-December SWE, 1-January SWE, and Peak SWE. We then calculated the ratios for 1-December and 1-January SWE relative to the peak value.
2.3 SNOTEL Observations
We repeated the calculations outlined above using observational data from the United States Department of Agriculture (USDA) National Resource Conservation Service SNOTEL Network and the British Columbia Cooperator Snow Sensors. These sites are typically located in small forest clearings in mountain terrain and generally consist of a pressure-based precipitation gauge filled with antifreeze, a temperature sensor, and a snow pillow that weighs the water content of the snow accumulated on top of it (Schaefer & Paetzold, 2001). Daily observations of mean air temperature, accumulated precipitation, and SWE were obtained for water years 2001-2022 for 873 sites across the western United States and Alaska. Only SWE measurements were available at 49 sites in British Columbia, Canada. At each U.S. site, daily mean air temperature was aggregated to mean per month and mean for January-February-March (JFM). Precipitation was aggregated to the amount accumulated between 1 October and 31 December (fall), and to the amount accumulated between 1 January and 31 March (winter). Correlation coefficients were calculated for fall and subsequent winter precipitation. Peak SWE each year was compared to the median and to a linear regression fit to 1 January SWE (Figures 1g, 1k, and 1o). For these, we calculated the mean absolute deviation (MAD) from the median, to assess interannual variability, and the mean absolute error (MAE) from the linear regression, to assess the skill in predicting peak SWE. We chose MAD and MAE over variance to minimize the effect of outliers. We calculated the difference (MAD-MAE) to assess the improvement in prediction skill added by the linear regression compared to the null hypothesis that the long-term median would be the best predictor of peak SWE each year.
Figure 1
(a) Western North America elevation map, highlighting locations of mountains, predominant stormtrack directions, and locations of three example sites (marked with numbers). (b) Annual mean precipitation from 1991 to 2020 (PRISM, 2022), highlighting importance of mountains to precipitation patterns. (c) December average temperature from 1991 to 2020 (PRISM, 2022), highlighting gradients from the coast, across mountains and with latitude. Illustration of methods as applied to SNOwpack TELemetry sites: (d-g) 1. Granite Creek, Alaska, (h-k) 2. Meadows Pass, Washington, and (l-o) 3. Yount’s Peak, Wyoming. (a, e, and i) Water year snow water equivalent (SWE) from 2001 to 2022. Heavy black line shows the median, and vertical dashed lines indicate 1 December and 1 January. (b, f, and j) As in a, but SWE plotted as a fraction of the peak SWE for each water year. Horizontal dashed line indicates 50% of the annual total. (c, g, and k) Scatterplot of October-November-December (OND) precipitation versus January-February-March (JFM) precipitation. (d, h, and I) Scatterplot of SWE on 1 January versus peak SWE each year. Dashed lines represent the 1:1 line (black), the median peak SWE value (blue) and the linear regression of peak SWE as predicted from 1 January SWE (red). The mean absolute deviation (MAD) about the median and the mean absolute error (MAE) about the regression are included for reference.
3 Results
3.1 What Is the Median Fraction of Peak SWE on the Ground by 1 December and by 1 January?
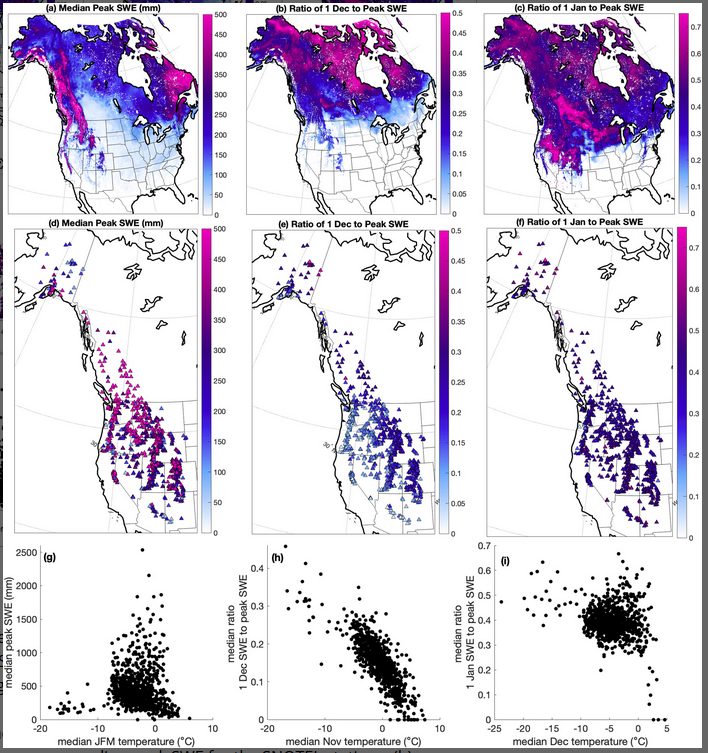
The fraction of 1 December SWE compared to peak SWE ranges from 0 to 0.6, with consistent patterns across model simulations and observations (Figure 2). The fraction increases with latitude, and within a given latitude, increases with elevation and distance from the coast. The fraction decreases with warmer November temperatures, with a statistically significant Spearman rank correlation coefficient of −0.82 (Figure 2h).
Figure 2
(a) Median modeled peak annual snow water equivalent (SWE), (b) Ratio of median modeled SWE on 1 December divided by values in (a), showing fraction of peak SWE on the ground on 1 December. (c) Ratio of median modeled 1 January SWE to peak SWE. (c, d, e) Same as for (a, b, c) but using observations at SNOwpack TELemetry (SNOTEL) and BC snow stations. (g) Scatterplot of median winter temperature versus median peak SWE for the SNOTEL stations. (h) Scatterplot of median mean November temperature versus median 1 December to peak SWE ratio for all SNOTEL stations, with a Spearman rank correlation coefficient of −0.82. Best fit slope to all values in (h) is −0.016 per °C. The best fit slope to temperatures above −5°C is −0.018 per ° C, and the best fit slope to temperatures below −5°C is −0.011 per °C. (i) Median December mean temperature versus 1 January to peak SWE ratio, with a Spearman rank correlation coefficient of −0.15. Note: Best fit line to the values at temperatures less than 0°C has a slope of −0.004 per °C. The best fit line to the values at temperatures greater than 0°C has a slope of −0.06 per °C, and at only temperatures greater than 2°C has a slope of −0.12 per °C.
By the end of December, the pattern of fractional SWE increasing to the north remains, and a pattern of increasing fractional SWE at interior locations emerges (Figures 2c and 2f). In the model simulations, many locations with less than 150 mm median peak SWE (Figure 2a) have over 60% of their peak SWE by 1 January (Figures 2c and 2f). Many of the highest fractional values are in the rain shadow of major mountain ranges, including interior Alaska, a band east of the Rocky Mountains from Saskatchewan, Canada to North Dakota, U.S., and the Northern Great Basin region east of the Sierra Nevada and Southern Cascade Mountains (Figure 2c). While the low altitude locations are not represented in the SNOTEL network, a similar spatial pattern appears, with lower fractions south of the Alaska range and higher fractions in the interior, with a gradient of lower fractions on the western slopes of the Cascades to higher fractions on the eastern slopes (Figure 2f). Many of the highest fractions in the lower-48 states are at locations near or bordering the Great Basin, in the same general area as highlighted in the model results. Model timeseries of SWE from example locations, as well as closer comparisons of model output and observations, are included in Supporting Information S1.
At locations with median December temperatures less than 0°C, the ratio of median 1 January SWE to peak SWE changes very little (slope of −0.004 per °C, Figure 2i). However, where median December temperatures are warmer than 0°C, the ratio decreases more rapidly as median temperatures increase (a slope of −0.06 per °C, Figure 2i). Sites with higher early season SWE fractions tend to be located in drier interior locations (Figure 1b), as discussed further in Section 4.
3.2 How Well Can Observed SWE on 1 January Each Year Predict Peak SWE?
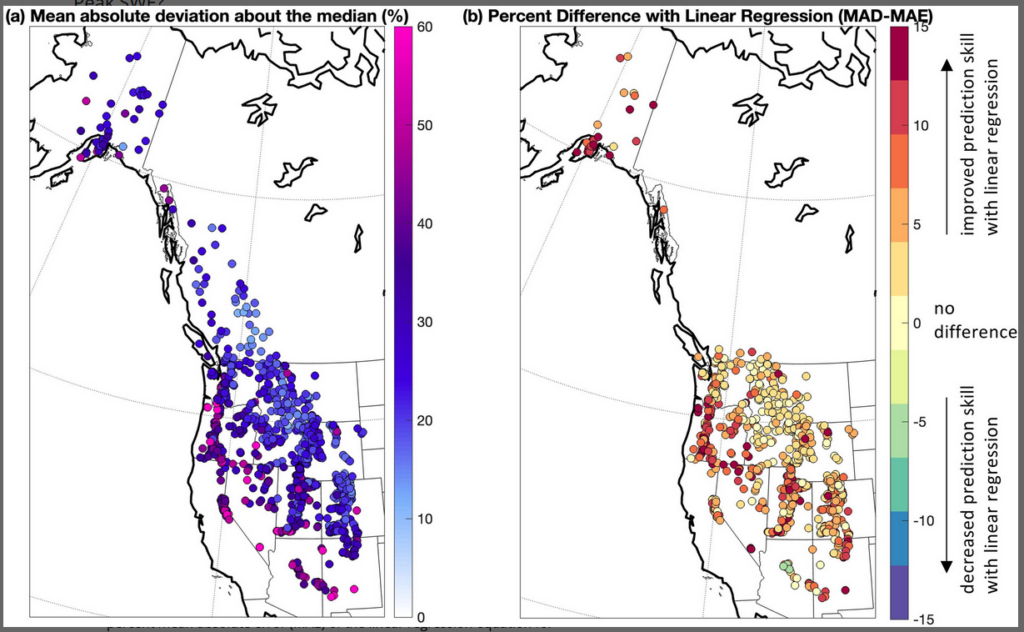
To understand predictability, we must consider that both the mean and variability of peak SWE differ greatly across locations. To establish a baseline for prediction, we calculate the interannual variability as the percent mean absolute deviation (MAD) in peak SWE compared to the observational median value (Figure 3a). Annual peak SWE is much more variable in California, Nevada, Arizona, and New Mexico, than in Washington, Idaho, Montana and British Columbia (Figure 3a). This is consistent with long-term evaluations of precipitation variability (Fatichi et al., 2012). Variability also increases in more coastal locations.
Figure 3
(a) Percent mean absolute deviation (MAD) in annual peak snow water equivalent (SWE) compared to the median. (b) Difference between the percent MAD and percent mean absolute error (MAE) of the linear regression equation for predicting peak SWE from 1 January SWE. Positive values indicate that MAE is less than MAD, while negative values indicate that MAE is greater than MAD.
Given this baseline, we assessed the percent MAE of predictions from a linear regression using observed 1 January SWE as a predictor (e.g., Figures 1g, 1k and 1o) and compared those to mean absolute deviation (MAD) about the median (Figure 3b). The linear regression improved prediction skill by greater than 10% at many sites in Alaska, Washington, and Oregon, as well as in Utah, Wyoming, Colorado, and northern New Mexico (Figure 3b). Sites with very low interannual variability, for example, much of Idaho and Montana, eastern Washington and northwest Wyoming, had relatively small deviations from the median and less than 10% improvement when using a linear regression. California, much of Nevada, and Arizona had high interannual variability, relatively high errors from using the median as a predictor, and, with the exception of a few sites, small or no improvement from using a linear regression. Very few BC snow sites had long enough records to perform a linear regression.
3.3 What Factors Explain Spatial Variations in the Predictive Skill of Early Season Snow?
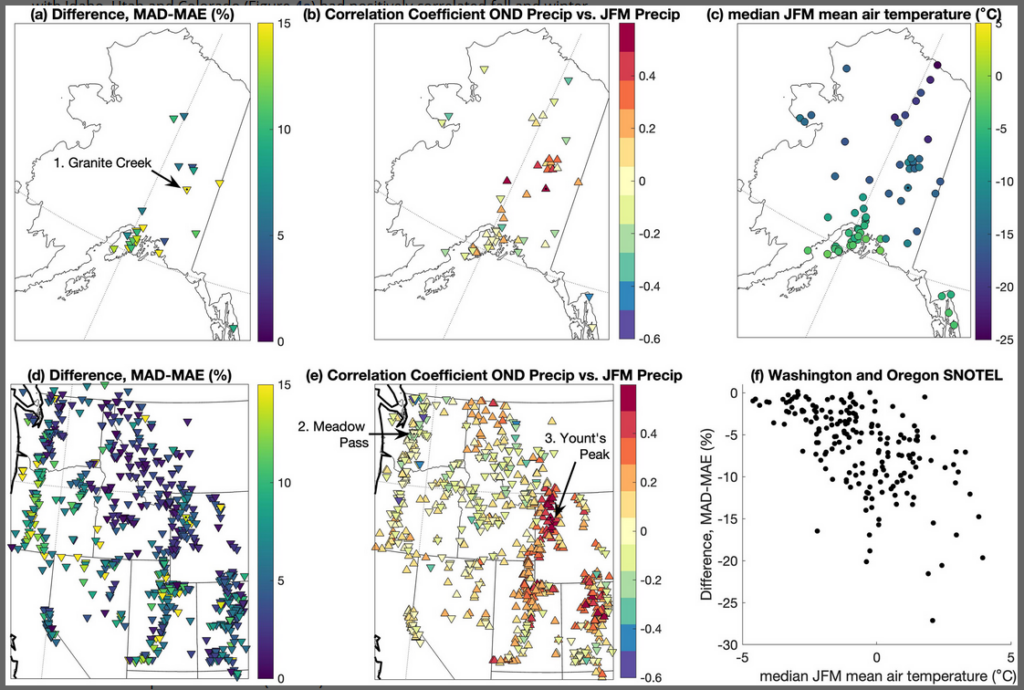
To better understand spatial variations in predictability, we empirically compared spatial patterns in MAD minus MAE to spatial patterns in the correlation coefficient between fall (OND) and winter (JFM) precipitation and to spatial patterns in JFM temperatures (Figure 4). Many of the SNOTEL stations in interior Alaska (Figure 4b) and along the border of Wyoming with Idaho, Utah and Colorado (Figure 4e) had positively correlated fall and winter precipitation. Many sites within these areas did not have high interannual variability, and thus, MAD’s from the median were less than 20% (Figure 3a), such that the linear regression made small additional improvements. However, individual sites in these areas, such as Yount’s Peak (Figures 1l and 1o), with higher interannual variability, had reductions in error of up to 20% using a linear regression.
Figure 4
For SNOwpack TELemetry (SNOTEL) sites, (a and d) the difference between mean absolute difference (MAD) about the median and mean absolute error in regression-estimated annual peak snow water equivalent (SWE), as a percent of the median peak SWE value. (b and e) Correlation coefficients between October-November-December and January-February-March precipitation. In general, values between ±0.4 were not statistically significant. Example sites from Figure 1 are marked. (c) Map of median JFM mean air temperature across Alaska. (f) Scatterplot of the median JFM mean air temperature versus MAD-MAE (from d) for SNOTEL sites in Washington and Oregon states. Spearman’s rank correlation coefficient is −0.61. Best fit slope to all values is −1.5% per °C, and to only mean temperatures greater than 1°C is −2% per °C.
Many sites in Washington and Oregon, including Meadow Pass (Figures 1j and 1k) showed decreased MAE compared MAD (Figure 4d), but these areas had either no significant correlations, or negative correlations, between fall and winter precipitation (Figure 4e). Within these states, the magnitude of error reduction was correlated with mean winter temperatures, with a Spearman’s rank correlation coefficient of −0.61 (Figure 4f). A similar pattern was found for sites on the southern side of the Alaska Range (Figures 4b and 4c). These sites experience frequent mixed precipitation (both rain and snowfall) and frequent midwinter melt.
With the exception of one site in southern Nevada and a couple sites in New Mexico, the areas with the greatest interannual SWE variability (i.e., greatest MAD) had no or very small improvements in predictability when using a regression on 1 January SWE (Figure 3). Many of these sites, for example, those in California, Arizona, and New Mexico, had warm winter temperatures, but the magnitudes of these temperatures were not correlated with error reductions as in the more northern states.
4 Discussion
4.1 Understanding Spatial Patterns of Where Early Season Snow Contributes the Most to Peak SWE
The importance of early season snow depends on sufficient precipitation and cold enough temperatures to accumulate snow in the fall, as well as the relative timing of snowfall and of snowmelt throughout the rest of the season. Precipitation depends on storm tracks and moisture availability. Across western North America, most moisture originates from the Pacific, and Pacific storm track locations shift from north to south as the water year progresses (Figure 1a and Supporting Information S1), with most storms making landfall in Alaska in early fall, and most storms impacting southern Oregon in January and February (Gershunov et al., 2017; Hoskins & Hodges, 2019a, 2019b; Mundhenk et al., 2016). Thus, due to precipitation alone, we would expect early season snowfall to be a greater fraction of the total in more northerly latitudes. Decreasing temperatures with latitude also contribute to early season precipitation falling as snow rather than rain, and contribute to that snow accumulating on the ground rather than melting. These latitudinal patterns are evident in the 1 December to peak SWE ratio (Figures 2b and 2e).
The 1 January to peak SWE ratio (Figures 2c and 2f) illustrates that beyond the influence of stormtrack latitude and temperature, December snowfall contributes the majority of annual SWE in multiple interior locations where nearby mountains block general moisture transport. These are locations with shallow snowpacks and minimal winter precipitation (Figure 1b), which typically only get one to two snowstorms per year, compared to six to 30 snowstorms per year in nearby mountain locations (Changnon et al., 2006). The stripe of high early season SWE fraction along the eastern flank of the Canadian Rockies through Saskatchewan and stretching southeast to North Dakota represents moisture that arrives through gaps in the mountains that occur north of 50°N (Liu & Stewart, 2003). Thus, this area receives moisture in November and December as the storm tracks shift south (Hoskins & Hodges, 2019b) but receives less moisture transport in the January-February-March period. Therefore, in these cold, dry interior locations, early-winter SWE is a good predictor of peak SWE because most of the limited snowfall occurs early in the winter.
The maximum intensity of integrated water vapor transport, associated with the strongest winds, in the latitudes of British Columbia, Washington, and Oregon occurs during the October to December period, leading to the farthest inland penetration of water vapor during that time (Gershunov et al., 2017; Rutz et al., 2014). This likely explains many sites in the Great Basin region (Figure 2c) that have >50% of median peak SWE occurring before 1 January.
Beyond changing interior moisture delivery, the shallow snowpacks in many locations in the Great Basin and leeward of the Rocky Mountains are subject to midwinter sublimation or melt. Model timeseries from point locations within the zone east of the Rocky Mountains where median 1 January SWE closely equals median peak SWE (yellow stripe, Figure 2c) reveal that the majority of snow accumulates during December each year, and this snow typically ablates completely in late January or early February (see Supporting Information S1). This area of prairie snow is referred to by Gray (1970) as the Chinook belt because warm dry strong winds frequently sublimate or melt out the snow midwinter (Pomeroy & Gray, 1994), as illustrated with detailed observations by MacDonald et al. (2018). Snowstorms occur again in March and April, but modeled spring SWE melts out quickly, and SWE values do not reach magnitudes as large as those on 1 January. Therefore, peak SWE is well-predicted by 1-January SWE at these ephemeral snowpack sites because peak SWE usually occurs close to 1 January.
4.2 Explaining Correlation of Early Season Snowfall to Subsequent Snowfall
Many of the areas where early season snowfall predicts subsequent snowfall are in regions where large scale circulation patterns influence snowfall similarly throughout the water year. Water vapor transport and thus, spatial distributions of precipitation and snowfall, are heavily influenced by sea surface temperature patterns, which change on annual or longer timescales. Gershunov et al. (2017) found that the largest correlation between Pacific coastal water vapor transport and sea surface temperatures occurred with a sea surface temperature pattern closely matching the Pacific Decadal Oscillation, PDO (Mantua & Hare, 2002; Newman et al., 2016). The warm-phase PDO is correlated with warmer temperatures across Alaska, but the cold-phase PDO is correlated with increased precipitation in interior Alaska (Hartmann & Wendler, 2005; Winski et al., 2017). Recent years with high snowfall in both the early and later seasons in interior Alaska (2018, 2020, 2022) have occurred during the cold-phase PDO, which is associated with the Pacific North Atlantic pattern shifting the dominant atmospheric pressure ridge in the Pacific to the west, which increases the probability of water vapor transport not being blocked by the Alaska range, allowing heavy winter precipitation in Fairbanks (L’Heureux et al., 2004). Thus, regions of interior Alaska have seasonal predictability (Figures 4a and 4b).
Sea surface temperature patterns have also been related to the likelihood of Pacific storms bringing moisture to interior locations in the western U.S. The second-largest correlation found by Gershunov et al. (2017) relates anomalous warmer temperatures in the western equatorial Pacific with increased precipitation near Wyoming, highlighting the same area where OND and JFM precipitation are significantly correlated (Figure 4e). This pattern differed from the more canonical El Nino Southern Oscillation (ENSO) pattern and warrants further investigation. While several studies have linked ENSO with stormtrack orientations and the amount of moisture propagating inland of the Cascade Mountain range (Siler et al., 2013; Wise & Dannenberg, 2017), we did not see significant correlations between fall and winter precipitation east of the Cascades (Figure 4e). Snowpack correlations in Washington seemed more related to temperatures and the likelihood of midwinter melt (Figure 4f).
4.3 Explaining Correlation of Predictive Skill and Midwinter Temperatures
Raleigh et al. (2015) found that a precipitation (snowfall) bias was the most important factor determining biases in melt rates. This occurs because greater amounts of snow take more energy to warm to isothermal at 0°C before melt can occur. Jennings et al. (2018) similarly found that the amount of snowfall was the best predictor of a snowpack’s cold content. Thus, in locations where temperatures are warm enough for midwinter melt to occur, greater snow accumulation in the fall is likely to lead to a decreased probability of midwinter melt and a higher peak SWE. Low snow accumulation in the fall is more likely to melt midwinter, making any subsequent snowfall still result in a lower peak SWE. Improved predictability in peak SWE as a function of 1 January SWE was correlated with mean winter temperatures in northern maritime regions (Washington, Oregon, and southern Alaska) but not in more southern regions because peak SWE in southern regions varies more according to highly variable snowfall in January through March than from melt.
4.4 Implications for Climate Change
While spring trends toward earlier snow disappearance have been observed globally, the date of fall snow onset is variable, without clear trends (Bartlett et al., 2005; Bormann et al., 2018; Notarnicola, 2020; Zhang, 2005). Climate models project the snow onset date to become later (Lader et al., 2020), and based on the sensitivity of 1 December SWE fractions to November temperatures (Figure 2h), we can expect very early season snowfall to decrease overall, leading it to be a smaller fraction of peak SWE. However, climate models also project a northern shift in storm tracks and an increase in fall precipitation in Alaska and northern Canada (Harvey et al., 2020), so in those areas that remain cold enough for precipitation to fall as snow, early season snowfall will likely become a greater fraction of peak SWE.
Warming temperatures will increase the likelihood of midwinter melt, which will likely increase the importance of early season SWE, particularly for deeper snowpacks with more cold content, in influencing the probability of early melt and hence, the resulting peak SWE. Overall, this is expected to increase both interannual variability and seasonal predictability, where larger early-season snow years will likely gain more snow overall than lower early-season snow years.
4.5 Implications for Ecosystems and Wildlife
Changes in spring melt timing are causing well-documented ecological responses in alpine and arctic ecosystems, but the implications of changes in fall snow on ecosystems are less well understood (Ernakovich et al., 2014). On a seasonal basis, earlier snowfall represents greater total insulation than later snowfall (Slater et al., 2017). The insulation effect of snow cover reaches a maximum in November (Zhang, 2005), and changes in fall conditions affect soil temperatures more than snow cover duration (Bartlett et al., 2005), with snow depths less than about 30 cm leading to frozen soils (Brooks & Williams, 1999; Slater et al., 2017). In Utquiavik, Alaska, shifting snow onset 1 week earlier in the fall made no difference in soil temperatures, but shifting it a week later let soil encounter colder air temperatures, leading to colder soils for the entire season (Ling & Zhang, 2003). Soil freezing affects permafrost (Cheng & Wu, 2007), methane fluxes (Mastepanov et al., 2013), water availability for carbon cycling (Brooks et al., 2011), and microbial activity (Brooks & Williams, 1999; Zhang, 2005). Snow insulation, or its absence, also influences animals that live under the snow or feed on vegetation under the snow (Berteaux et al., 2017). Finally, Cosgrove et al. (2021) found that fall snow depth and fall air temperature explained 41% of the variance in Dall sheep reproduction in Alaska and that winter and spring values of snow depth and density could be predicted from fall conditions. This suggests that for northern regions, fall snow conditions can be used to predict likely impacts on wildlife in spring and plan appropriate management strategies.
5 Conclusions
Early season snow accumulation provides some predictive potential for peak SWE accumulation across much of North America. In locations where a greater fraction of total SWE accumulates early in the season, the peak SWE is more predictable simply because the majority of it has already accumulated, and the future will have less influence. The fraction of early season SWE relative to peak SWE increases with latitude and in locations with cooler fall temperatures. It also increases in interior locations, where mountains frequently block moisture flow, and winter downslope (e.g., Chinook) winds melt or sublimate shallow snowpacks. In these locations, the snow on the ground by the end of December is close to the peak snow accumulation.
As discussed in Section 4.2, above-average early season SWE indicates in many locations that sea surface and large-scale atmospheric conditions are favorable for snowfall, and later season snow accumulation is also likely to be above average. Conversely, in locations with winter temperatures conducive to melt, low SWE in the early season leads to a higher probability of mid-winter melt, which contributes to lower peak SWE. This increases predictability in warmer northern states but not in southern states, where high variability in later-season precipitation has a greater influence on peak SWE. Combined, these factors lead to extreme early seasons leading to more extreme peak SWE distributions. Both the extremes and the relationships between fall and winter conditions are expected to strengthen as temperatures warm, so understanding these relationships will help with predictability and human and wildlife adaptations.
Acknowledgments
This research was funded by NASA Interdisciplinary Research in Earth Science (IDS) Grants 80NSSC20K1291 to JDL and LRP and 80NSSC20K1292 to MD. Special thank you to Mark Raleigh for sharing Matlab code to download SNOTEL data and to John Pomeroy for sharing references about Chinook winds in the Canadian prairies. We thank schools and childcare providers for staying open, enabling parents to work. We thank A. Shcherbina for help with map projections and colorbars and L. VanWagtendonk for help with figure organization. We also thank the University of Washington’s ADVANCE Write Right Now program, which provides a structure to help busy professors focus on writing, which was essential for this paper.
Lundquist, J. D., Kim, R. S., Durand, M., & Prugh, L. R. (2023). Seasonal Peak Snow Predictability Derived From Early-Season Snow in North America. Geophysical Research Letters, 50(17), e2023GL103802. https://doi.org/10.1029/2023GL103802
–
I hope you found this article interesting and useful. –

Happy Hanukah Sig.
Thank you and Happy Holidays to your family. I hope you liked that article but it does not much apply to NM except the highest peaks. It may apply to fewer places this year with the rapid transition to and then away from La Nina conditions.
I hope you also enjoyed my economic analysis of cloud seeding article. New Mexico is determined to not have the water it needs for some strange reason but the rest of the West and much of the world is using cloud seeding to increase precipitation. Eastern NM is culturally part of Texas so they are keen to use cloud seeding.